Simplifying Radicals Using Perfect Square Factors
Learn how to simplify radicals by using perfect square factors. Understand the concept of perfect squares, identify perfect square factors, and follow steps to simplify radicals with examples provided in this educational material.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
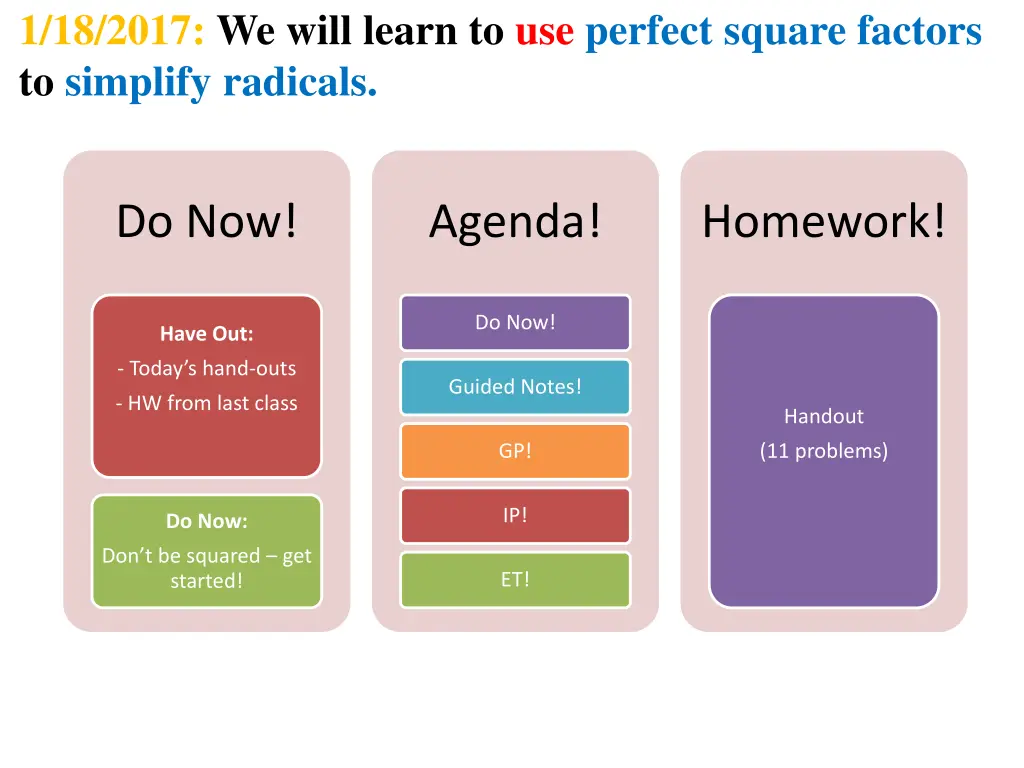
1/18/2017: We will learn to use perfect square factors to simplify radicals. Do Now! Agenda! Homework! Do Now! Have Out: - Today s hand-outs Guided Notes! - HW from last class Handout (11 problems) GP! IP! Do Now: Don t be squared get started! ET!
We will learn to use perfect square factors to simplify radicals. Hook Hook: : How are these How are these equivalent 45 = 3 5 equivalent? ?
Introduction Numbers like 1, 4, 9, 16, 25, 36, etc. are called _______________ because they are the product of an integer times itself. perfect squares EX: 4 4 or 42 = 16 When you take the square root of a perfect square, the result is a _____________. whole number EX: 16 =4
Not a perfect square? 1. What 2 integers is between? (Mental Math) 8.66 75 8 and 9 (Because 82 = 64 and 92 = 81) 2. What is the approximate value of ? (Calculator) 75 3. We can also simplify the radical
Background Vocabulary radical radicand This is also called a Square Root
Steps to Simplify Radicals 1. Find the largest __________________ of the radicand, excluding 1. perfect square factor Note: A factor is a number that divides evenly into a given number with no remainder. 2. Write the number as the _______ of the perfect square factor and its other factor. product 3. Split each factor into two separate _______. radicals 4. Simplify the _____________ radical. perfect square
Example 1: 75 1. Find the largest perfect square factor of 75, excluding 1. Check for perfect square factors of 75: 4, 16, 25, 36, 49, 64 2. Write the radicand as the product of the perfect square factor and its corresponding factor. 75 3 25
Example 1: 3. Split each factor into two separate radicals. 3 25 3 25 75 3 3 4. Simplify the perfect square radical. 5 5
24 23 Example 2: First Step: Multiply the radicals 72 Then try to simplify on your own Lastly, check if you have the same answer as your neighbors.
Discussion Questions 1. What happens if you do not use the largest perfect square factor when simplifying? The radicand will still have perfect square factors and can be further simplified by repeating the process. 2. What if the radicand does not have any perfect square factors other than 1? The radical is already in simplest form.
More Simplification What if the number under the radical is a fraction?
Example 3: Rationalizing the Denominator 16 3 16 3 1. Separate the numerator and denominator into separate radicals. Is this radical in simplest form? 4 2. Simplify each radical if possible. 3 We must rationalize the denominator. No, we cannot have a radical in the denominator.
Example 3: Rationalizing the Denominator 4 3 3 3. Multiply both the numerator and denominator by the root. 3 Why can we do this without changing the result? 4. Simplify. 4 3 3
Example 4: Rationalizing the Denominator 27 2 27 2 Simplify the radical. = 9 3 2 9 3 2 =3 3 = = Rationalize the denominator. 2 =3 3 2 2 2 =3 6 2