Solid Generation and Volume Calculation Methods in Mathematics
Explore examples of finding volumes of solids generated by revolving regions around axes using various methods like disks, washers, and cylindrical shells in calculus. Understand how to calculate volumes using integration and cylindrical shell formulas.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
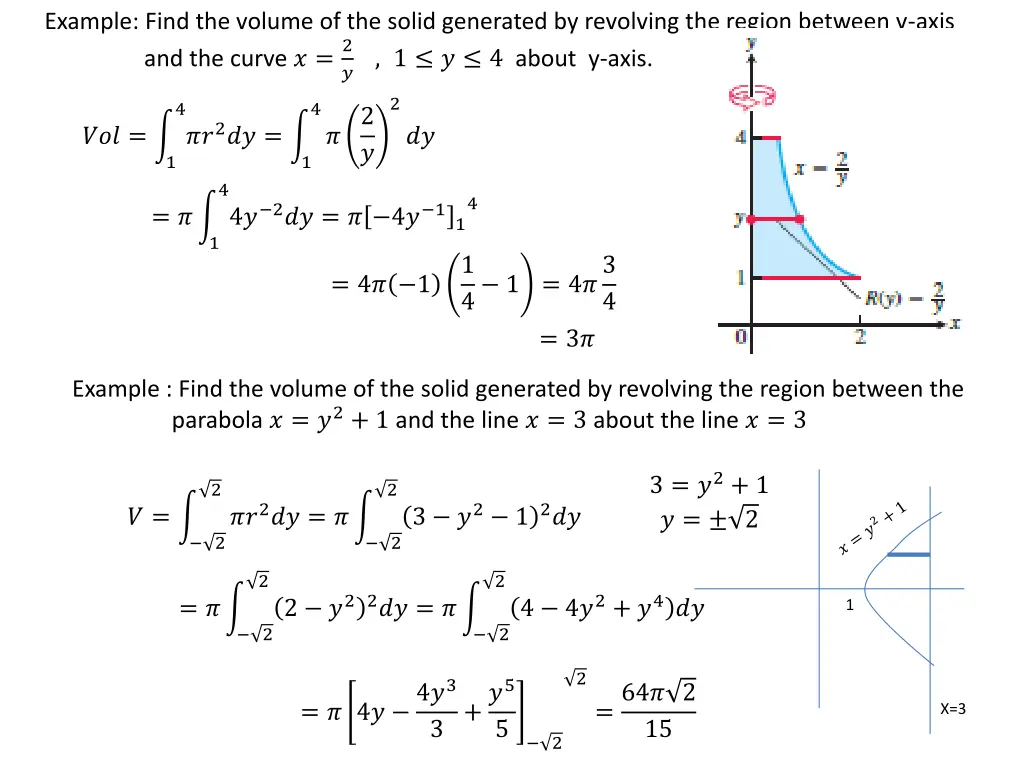
Example: Find the volume of the solid generated by revolving the region between y-axis and the curve ? = ? , 1 ? 4 about y-axis. 2 2 4 4 2 ? ??2?? = ??? = ? ?? 1 1 4 4 4? 2?? = ? 4? 1 = ? 1 1 1 4 1 = 4?3 = 4? 1 4 = 3? Example : Find the volume of the solid generated by revolving the region between the parabola ? = ?2+ 1 and the line ? = 3 about the line ? = 3 3 = ?2+ 1 ? = 2 2 2 ??2?? = ? 3 ?2 12?? ? = 2 2 2 2 2 ?2 2?? = ? 4 4?2+ ?4?? = ? 1 2 2 2 = ? 4? 4?3 +?5 =64? 2 15 X=3 3 5 2
Washer method If the region we revolve to generate a solid does not border on or cross the axis of revolution , the solid has a hole. The cross sections are washers instead of disks. Example: The region bounded by the parabola ? = ?2 and the line ? = 2? in the first quadrant is revolved about the y-axis to generate a solid. Find the volume of the solid. 2? = ?2 ?2 2? = 0 ? = ?2 ? ? 2 = 0 ? = 0, ? = 2 4 4 ? ?2 ?2 (? 2)2?? = ? ? = ? ?? 4 0 0 4 ?2 2 ?3 =8 = ? 3? 120
Example: Find the volume generated by revolving the area enclosed by ? = ?2+ 1 ,? = ? + 3 about the x-axis ?2+ 1 = ? + 3 ? = ?2+ 1 2 ?2 ? 2 = 0 ? = 2,? = 1 ? ?2 ?2?? ? = 1 -1 2 2 ? ? + 32 ?2+ 12?? = 1 2 2 ? ?2+ 6? + 9 ?4 2?2 1 ?? = ? ?2+ 6? + 8 ?4?? = 1 1 2 = ? ?3 3+ 3?2+ 8? ?5 = 21? 5 1 Example: Find the volume of solid generated by revolving the region by ? = ?2 and ? = ? about the x-axis. ?2= ? ? = 1,? = 1 1,1 1 1 ?2 2 ?3 =? ? ? ?2?? = ? ? = 3 6 0 0
Volumes using Cylindrical Shells ?? ? ?? , where A(x) is an integral The volume of a solid as the definite integral ? = ? cross sectional area of the solid. The area A(x) was obtained by slicing through the solid with a plane perpendicular to x-axis. However, this method of slicing in sometimes awkward to apply . To overcome this difficulty, we use the same integral definition for volume in different way by using Cylindrical Shells method. Example: Find the volume generated by revolving the region enclosed by the parabola ? = 3? ?2 ????? ? ? ? = 1 ?? ??= 3 2? = 0 3? ?2= 0 ? 3 ? = 0 ? =3 2 ??? ? =9 ? = 0 ??? ? = 3 3 2,9 4 ? ???. 4 ???? = 2? ? ??? ?????? ? ??? ??? ? ???? = 2? ? + 1 ? -1 y x 0 ? ?? ? + ? ?? ???? ? = ? 3 2? 3?2 ?3+ 3? ?2?? ? = 0 3 2?2 ?4 2 3?3+3 =45? = 2? 4 2 0
Example: Use cylindrical shell method to find the volume of the solid generated when the region enclosed by ? = ? ??? ? = ?2 is revolved about y-axis. ? = ?2 ? 1 ? = 0 ? = 0 ?? ? = 1 y=x 1 1 2?? ? ?2?? ? = 2????? = x ? = ?2 0 0 1 1 ?3 3 ?4 =? ?2 ?3?? = 2? = 2? 4 6 0 0 Example: Use Cylindrical Shell to find the volume of the solid generated when the region under ? = ?2 over the interval (0, 2) is revolved about x-axis. 4 4 ? = 2????? = 2? ? 2 ? ?? x 0 0 y 4 4 0 2 3 2 ?? = 2? ?2 2 =32? 5 2 = 2? 2? ? 5? 5 0 0