Solution to Nonlinear Equation and Initial Value Problem: Implicit vs. Explicit
Explore the solution to a first-order nonlinear equation involving implicit and explicit differentiation techniques, along with initial value problems. Understand the process of separating variables and using calculus to find the solutions explicitly. Learn about domains and conditions affecting the solutions in this comprehensive analysis.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
http://bcs.wiley.com/he-bcs/Books?action=resource&bcsId=2026&itemId=047143339X&resourceId=4140http://bcs.wiley.com/he-bcs/Books?action=resource&bcsId=2026&itemId=047143339X&resourceId=4140 Example 2: Implicit and Explicit Solutions (1 of 4) Solve the following first order nonlinear equation: 2 4 3 y dx + + 2 dy x x = ( ) 1 2 Separating variables and using calculus, we obtain ( ) ( ) x x dy y + + = 2 2 2 ( ) = + + 2 2 1 3 4 2 y dy x x dx If you can solve for y, you must do so and give explicit answer. ( ) 2 2 1 3 4 2 dx = + + + 2 3 2 y y x x x C The equation above defines the solution y implicitly. An explicit expression for the solution can be found in this case: ( C x x x y y = + + + 0 2 2 2 ( ) + + 2 + + 3 2 ) 2 4 4 2 2 x x x C = 2 3 2 y = + + + 3 2 1 2 2 y x x x C
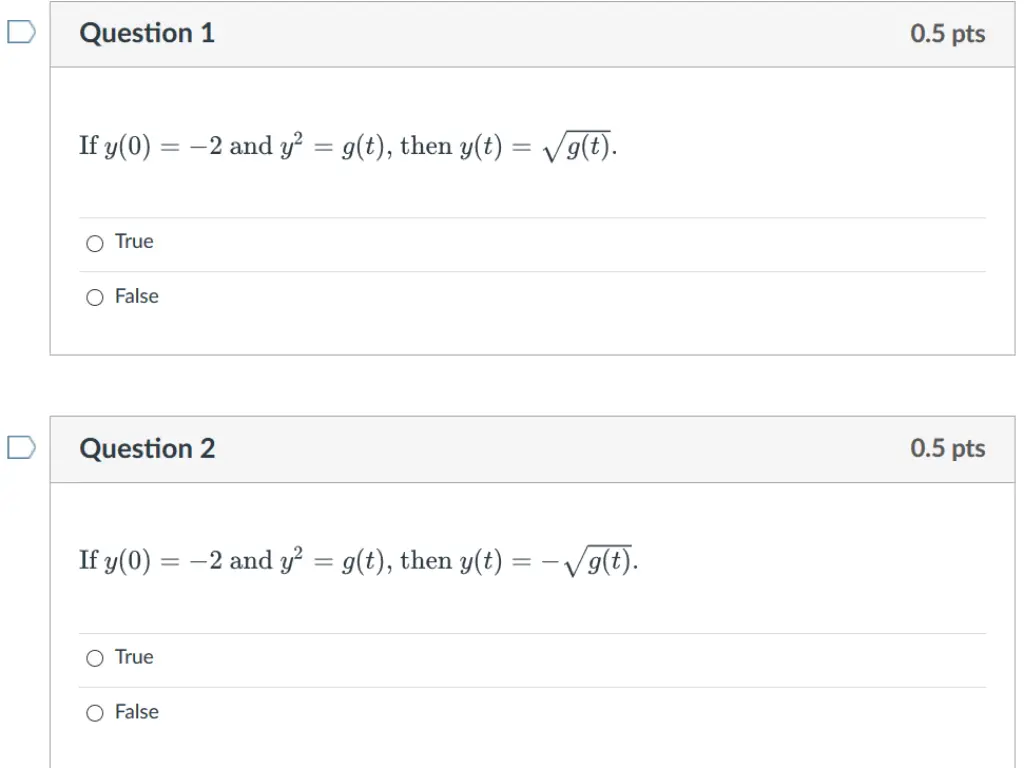
http://bcs.wiley.com/he-bcs/Books?action=resource &bcsId=2026&itemId=047143339X&resourceId=4140 Example 2: Initial Value Problem (2 of 4) Suppose we seek a solution satisfying y(0) = -1. Using the implicit expression of y, we obtain 2 2 2 = = C C In this class (and in many applications), solutions will always be functions (and thus satisfy vertical line test). = + + + 2 3 2 y y x x x C 2 ( ) 1 ( 2 ) 1 3 Thus the implicit equation defining y is = + + + 2 3 2 2 2 2 3 y y x x x Using explicit expression of y, = + + + 3 2 1 2 2 = y x x x C = 1 1 4 C C It follows that = + + + 3 2 1 2 2 4 y x x x
http://bcs.wiley.com/he-bcs/Books?action=resource &bcsId=2026&itemId=047143339X&resourceId=4140 Example 2: Initial Condition y(0) = 3 (3 of 4) Note that if initial condition is y(0) = 3, then we choose the positive sign, instead of negative sign, on square root term: = + + + + 3 2 1 2 2 4 y x x x In this class (and in many applications), solutions will always be functions (and thus satisfy vertical line test). Domain will always be a single open interval.
HW hint: For one of your HW problems, to find domain: 1. Determine where tangent line is vertical. For this particular problem, this will occur at certain y-values. 1. Plug these y-values into solution and solve for x to find potential boundary of domain. Note: Domain will always be a single open interval.
http://bcs.wiley.com/he-bcs/Books?action=resource &bcsId=2026&itemId=047143339X&resourceId=4140 Domain will always be a single open interval. Example 2: Domain (4 of 4) Thus the solutions to the initial value problem 2 4 3 y dx + + 2 dy x x = = , ) 0 ( y 1 ( ) 2 1 are given by 2 y = + + + 3 2 2 2 2 (implicit) 3 y x x x = + + + 3 2 1 2 2 4 (explicit) y x x x From explicit representation of y, it follows that ( ) ( 2 2 1 + + + = x x x y )( ) 2 ) ( = + + 2 2 2 1 2 x x and hence domain of y is (-2, ). Note x = -2 yields y = 1, which makes denominator of dy/dx zero (vertical tangent). Conversely, domain of y can be estimated by locating vertical tangents on graph (useful for implicitly defined solutions).
http://bcs.wiley.com/he-bcs/Books?action=resource&bcsId=2026&itemId=047143339X&resourceId=4140http://bcs.wiley.com/he-bcs/Books?action=resource&bcsId=2026&itemId=047143339X&resourceId=4140 Example 3: Implicit Solution of Initial Value Problem (1 of 2) Consider the following initial value problem: cos 3 = + y y x = , ) 0 ( y 1 y 1 3 Separating variables and using calculus, we obtain y = cos + 3 1 3 dy xdx y 1 + = 2 3 cos y dy xdx y + = + 3 ln sin y y x C Using the initial condition, it follows that + = + 3 ln sin 1 y y x Implicit solution
http://bcs.wiley.com/he-bcs/Books?action=resource &bcsId=2026&itemId=047143339X&resourceId=4140 Example 3: Graph of Solutions (2 of 2) Thus cos + y x = = + = + 3 , ) 0 ( y 1 ln sin 1 y y y x 3 1 3 y The graph of this solution (black), along with the graphs of the direction field and several integral curves (blue) for this differential equation, is given below. Solutions vary dramatically based on initial value.
Force due to air resistance Gravitational force ? = ? + ?? where ? = ? ? < 0 Thus solutions converge to equilibrium solution Equilibrium solution: v = C Note C is the limiting velocity.
) - predation ( or proportionality constant ? > 0 Thus solutions diverge from equilibrium solution
If rate of change proportional to S:
We will use this in section 3.7 ?2 + ?2 =
HW hint (#4): Simplify your answer. https://www2.clarku.edu/ faculty/djoyce/trig/identiti es.html
https://www.math.net/arcsin y = arcsin(x) Ex: If sin(x) = 0, then x = arcsin(0) + k = k Ex: If sin(x) = 1/2, then since arcsin(1/2) = /6 x = /6 + 2 k = arcsin(1/2) + 2 k or x = 5 /6 + 2 k = (arcsin(1/2) + 4 /6) + 2 k = ( - /6) + 2 k = ( - arcsin(1/2)) + 2 k https://www.symbolab.com/
If sin(x) = c, then x = arcsin(c) + 2 k or x = ( - arcsin(c)) + 2 k
Section 2.1 You canNOT use formula. You must show product rule step.
HW hint If taking limit, might be able to use l hopital s rule and


