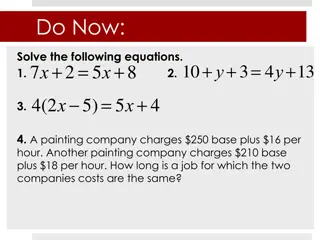Solving Exponential Equations Algebraically
Learn how to solve exponential equations algebraically with the same base and unlike bases. Understand the properties of equality for exponential equations and practice solving various equations step by step. Improve your skills in rewriting equations with the same base and applying the rules of exponents to find the solutions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
6.5 Solving Exponential Equations How can you solve an exponential equation algebraically? 1. Students will be able to solve exponential equations with the same base. 2. Students will be able to solve exponential equations with unlike bases.
1. Students will be able to solve exponential equations with the same base. Solving Exponential Equations with the Same Base Property of Equality for Exponential Equations Two powers with the same positive base b, where ? 1, are equal if and only if their exponents are equal. If 2?= 25, then ? = 5. If ? > 0 and ? 1, then ??= ?? if and only if ? = ?.
1. Students will be able to solve exponential equations with the same base. Solving Exponential Equations with the Same Base Solve each equation 6 = 62? 3 1 = 2? 3 4 = 2? 2 = ? must equal each other. 103?= 102?+3 3? = 2? + 3 ? = 3 same the exponents must equal each other. 3?+1= 35 ? + 1 = 5 ? = 4 same the exponents must equal each other. Since the bases are the Since the bases are the same the exponents Since the bases are the
You Try!! Solve each equation 22?= 26 2? = 6 ? = 3 73?+5= 7?+1 3? + 5 = ? + 1 2? + 5 =1 2? = 4 ? = 2 52?= 5?+1 2? = ? + 1 ? =1
2. Students will be able to solve exponential equations with unlike bases. Solving Exponential Equations with Unlike Bases To solve some exponential equations, you must first rewrite each side of the equation using the same base. 5?= 125 5?= 53 ? = 3 the same can you write 125 as some power of 5? 4?= 2? 3 (22)?= 2? 3 22?= 2? 3 2? = ? 3 ? = 3 9?+2= 27? (32)?+2= (33)? 32(?+2)= 33? 32?+4= 33? 2? + 4 = 3? 4 = ? Powers of 3! Since the bases are not Since the bases are not the same can you write 4 as some power of 2? Since the bases are not the same can you write 9 and 27 as the power of the same number?
You Try!! Solve each equation 4?= 326 (22)?= (25)6 22?= 230 2? = 30 ? = 15 43?= 8?+1 (22)3?= (23)?+1 26?= 23?+3 6? = 3? + 3 3? = 3 ? = 1 92?= 3? 6 (32)2?= 3? 6 34?= 3? 6 4? = ? 6 3? = 6 ? = 2
2. Students will be able to solve exponential equations with unlike bases. More Solving Exponential Equations with Unlike Bases To solve some exponential equations, you must first rewrite each side of the equation using the same base. 2)?= 4 (1 4?+1= 4?+1= 4 3 ? + 1 = 3 ? = 4 the same number? Powers of 4! 1 64 (2 1)?= 22 2 ?= 22 ? = 2 ? = 2 same number? Powers of 2! Since the bases are not the same can you write 1 and 4 as the power of the Since the bases are not the same can you write 4 and 1 2 64 as the power of
You Try!! Solve the equation 3)? 1= 27 (3 1)? 1= 33 3 ?+1= 33 ? + 1 = 3 ? = 2 ? = 2 (1
Lets Review 1. Students will be able to solve exponential equations with the same base. This is the easy one. If the bases are already the same the exponents must equal. Then solve for x. 2. Students will be able to solve exponential equations with unlike bases. This is the harder one. If the bases are not the same you have to think, what number raised to a power will equal the original base. You want to have both bases changed to the same base. Then the exponents must equal. Then solve for x.