Solving Linear and Quadratic Inequalities with Graphs
Learn how to solve linear and quadratic inequalities by visualizing them as graphs. Understand the concept of determining parts of the graph that satisfy the inequality conditions with step-by-step examples. Practice solving various types of inequalities and improve your understanding of discriminant nature.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
SECT. 4.5 THE DISCRIMINANT NATURE OF THE ROOTS
SOLVING LINEAR AND QUADRATIC INEQUALITIES One way to solve inequalities is to visualize it like a graph Suppose you are given the inequality below: The left side of the equation is a linear graph (straight line) The right side of the equation is a horizontal line (y=0) is the x-axis The inequality in the middle is looking for parts of the graph where the line is Greater (ABOVE) the X-axis! So where is your answer?? 3 4 0 x 3 4 x 4 3 Straight line: 3 x = 3 m = b = Hor. Line y = X-axis 0 4 y x 4 Your answer will be from the intersection point and greater b/c the red line is above the axis from here and beyond
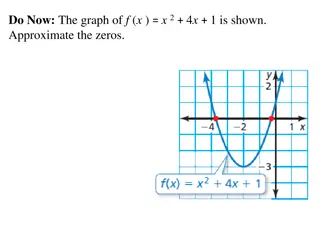
If you are solving a quadratic inequality, do the same thing and visualize as a graph The left side is a parabola, factor it to find the x-intercepts The right side, again, is the x-axis [y=0] The inequality says that we want parts of the graph where the parabola is greater (above) the x-axis! 1 + 2 3 )( 4 4 0 0 x ( x x ) x x = x = This is a parabola with x-intercepts at x=4 and x=-1 1 From the graph, you can see that the answer is the outside (left and right) 1 or 4 x 4 Your answer will be these two separate parts where the parabola is above the X-axis x
STEPSFOR SOLVING QUADRATIC INEQUALITIES: If linear, solve directly, If Quadratic move all terms to one side so that one side of the equation becomes zero (make it the x-axis) Solve for x these will become the intersection points Sketch the graph and use the inequality to determine if you are looking for parts that are Above Below or equal to the X-axis 8 4 0 x + 3 9 x + You want parts of the LINE that is LESS than and Equal to the X-axis X-axis + + 2 2 2 6 0 0 x You want parts of the PARABOLA that is ABOVE than the X-axis x You want parts of the PARABOLA that is LESS/UNDER than the
Practice: Solve each of the following inequalities x ) 3 b ( ) + 11 6 x+ )5 4 7 )2 3 15 0 x a c x ( )( ) + ) 2 1 4 3 0 2 d x x )2 10 e x x + + + 2 2 ) 2 3 0 ) 6 14 8 5 3 g x x f x x x
( ) ) 3 11 6 3 x + x 5 x+ )5 4 x 7 11 11 5 )2 3 15 0 b x a c x 5 This one is quadratic, so find the x-intercepts first x 5 3 3 5 3 x x = x = x+ 3 = 2 0 0 3 15 x = x = 0 15 5 3 x ( )( ) The part of the parabola that is UNDER the x-axis is in between the two roots 5 ) 2 1 4 3 0 d x x This one is quadratic, so find the x-intercepts first 2 1 0 x = 0.5 x = 0 x x = 4 3 x = 0 3 4 The part of the parabola that is ABOVE the x-axis is outside of the two roots (left/Right) 0.5 0.75 x or x
+ + 2 2 )2 10 ) 6 14 8 5 3 e x x f x x x This is also Quadratic, but you will need algebra to factor and find x-intercepts 2 2 10 x x + ( )( 2 5 2 x x + 2.5, x x = = 2 2.5 x This one obviously needs algebra to isolate and factor 2 6 11 x ( )( 3 1 2 x + 1 , 3 The part of the parabola that is ABOVE the x-axis is Outside the two roots 1 3 This one is a tricky one. If you CTS the eqn on the left, you realize that it is a parabola with no x-intercepts and is completely above the x-axis + 3 3 2 3 ) 0 0 x 2 0 0 x The part of the parabola that is under the x-axis is between the two roots ) = = x x 3 2 x or x + + + 2 ) 2 3 0 g x x ) ( 2 x+ 1 1 0 ! no solution Since the parabola is never under the x- axis b/c it opens up and shifted up, there will be no solution!
II) DISCRMINANT: NATUREOFTHE ROOTS In this next part of the lesson, we want to determine how many x-intercepts a QF will have by looking at the Discriminant The Discriminant will determine the Nature of the Roots , which refers to the Number of X-intercepts that a Quadratic Function will have A Quadratic function (Parabola) can have either 2 distinct roots (2 different x intercepts) 2 equal roots (1 distinct root, double root) No real roots (no x intercepts) Use the Discriminant Formula to find the Nature of the roots: 2 4a b b c = x = 2 4 D b ac 2 a The discriminant comes from your Quadratic formula! This is your discriminant formula
2 4 b ac II) DISCRMINANT y 2 1) 4 0 b ac 0 There will be 2 distinct roots - - x x -2 -1 0 1 2 = 2 y 2) 4 0 b ac 0 4 x There will be a double root/ 2 equal roots x 4 -1 0 1 2 3 y 2 3) 4 0 b ac x 4 x -2 -1 0 1 2
EX: DETERMINETHENATUREOFTHEROOTSFOR EACHEQUATION: (DONOT SOLVE) 2 ) 4 7 8 i x x + 4 7 8 , , a b c = = = + = + c 2 ) 3 3 5 , 5 12 1 = ii a x , x = 2 b = 2 = 2 4 D b ( ) 5 ac 4 D b ( ac ( )( ) 3 12 ) ( )( ) 4 4 8 2 2 D = D = 4 7 D = 25 144 + = D = 49 128 = 169 79 Discriminant is positive There are 2 real roots Discriminant is negative There are no real roots
ALTERINGTHE NATUREOFYOUR ROOTS In this next part, you will have an unknown constant k in your quadratic equation You want to know what values of k will there be: Case 1: 2 roots Case 2: 1 root or Case 3: Zero roots Suppose, we start with case 1 , for what values of k will there be 2 ROOTS? Treat the constant k like the variable x , our inequality becomes a quadratic equation 2 8 y x kx = + + so the discriminant must be greater than zero 2 4 b ( )( ) 4 2 8 0 k 2 64 0 k 8, 8 k k = = 8 8 k or k than -8 or bigger than 8, the QF will have We want the equation to have 2 different roots, 2 2 = = = 0 ac 2, , 8 a b k c The part of the parabola that is above the x-axis is outside (left and right) So this means that if k is either less 2 different roots
III) NATUREOF ROOTS (SOLVING FORK) Ex: For what values of k does the equation have two different real roots? + + = 2 2 8 0 x kx ( )( ) 4 2 8 k Since the equation has 2 different real roots, The discriminant must be greater than zero 2 4 b ac k 2 0 0 2 64 k 0 64 2 8 8 8 8 k or k IF K is less than -8 or greater than 8, the quadratic equation will have two X-intercepts
Practice: For what values of k does the equation have a) Two equal roots b)No real roots 2 9 2 4 0 x kx + = a) Since the equation has 2 equal roots, The discriminant must be equal to zero ( ) ( )( ) 2 4 9 4 0 k = 2 4 144 0 k = k = b) No real roots discriminant must be less than zero ( ) ( )( ) 2 4 9 4 k 2 0 2 k k 2 4 144 36 2 2 4 144 k = k = 2 36 6 6 6 6 k 6 IF K equals 6 or -6, the equation will have a double root! IF K is between 6 or -6, the equation will not have any roots
Practice: For what values of k does the equation have a) Two different roots b)No real roots ( ) 2 1 8 4 0 k x x + = a) the discriminant is greater than zero ( ) ( )( ) 8 4 2 1 4 0 k ( ) 64 16 2 1 0 k 64 32 16 0 k + 2 b) the discriminant is less than zero ( ) ( 8 4 2 64 16 2 64 )( ) 1 4 k k + 2 2 0 0 0 k ( ) 1 16 32 80 2.5 32k k 80 2.5 32k k If k is greater than 2.5, the function will have no roots If k is less than 2.5, the function will have two roots