Solving Quadratic Functions by Factoring
How to solve quadratic functions by factoring is essential in mathematics. This lesson covers the concept of solving equations, trinomials, and practicing with various examples to enhance your skills. It provides step-by-step explanations and visuals to help you grasp the process effectively.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
LESSON 2: SOLVING QUADRATIC FUNCTIONS BY FACTORING
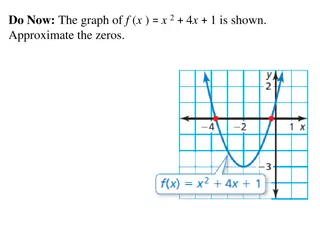
I) WHAT DOES IT MEAN TO SOLVE AN EQUATION? What Does Solving Mean? Answer: Finding a value for x (Variable) so that both sides of an equation will be equal Ex: Solve for x ( ) 2 2 1 5 + = 4 1 5 + = 5 5 = x+ = 2 2 1 x = x = 5 4 2 Both sides will be equal When you re solving there will always be an equal sign in the equation.
II) SOLVING TRINOMIALSBY FACTORING When you have the product of two brackets equal to zero, you can solve this equation easily: Rule: zero times anything is always equal to zero ( )( ) + = 3 2 5 0 x x Make each bracket equal to zero Solve for x from each bracket x = x = x+ = 2 5 0 3 x = 0 You get two answers, one from each bracket 2.5 3 Check: ( )( ) ( )( 3 ) + = = = = 3 2 )( + 5 0 x ( x + = ) 3 2 + 5 0 = = = x x ( )( 0 ) ( )( 5 3 5 8 0 5 0 0 0 3 6 5 11 0 0 0 ( )( ) ) 0 0
PRACTICE: SOLVEEACHOFTHEFOLLOWINGEQUATIONS ( )( ) = ) 3 4 5 0 ii x x 10 15 x = ) 7 i 4 x = x = x = 3 4 x = 0 4 4 3 5 0 0 x = 10 15 28 3 x = 10 43 43 10 x = = x = 4.3 Two values multiply to zero. Each value can be equal to zero. ( )( ) ( )( ) + = 3 8 + = ) 8 7 2 3 0 ) 4 5 0 iii x x iv x x x x = 3 8 3 = x+ = 4 x = 0 0 4 5 0 x x+ = 8 7 0 x = 2 2 3 x = 0 3 3 2 = 8x 5 5 4 x = 8 7 7 8 3 8 = = x x = x = x
When solving trinomials or equations with an x2, move all terms to one side and make it equal to zero, Then factor the equation to two binomials Make each binomial equal to zero Solve for x from each bracket = + 2 10 9 9 Ex: Solve for x x x = 2 10 9 9 0 x x Move all terms to the left and then factor ( )( ) Make each bracket equal to zero + = 2 3 5 3 0 x x Solve for x from each bracket x+ = 5 x = 2 5 3 x = x = 0 2 3 x = x = 0 3 3 3 5 1.5
PRACTICE: FACTORAND SOLVE ) 72 11 6 c c = + = 2 2 ) 8 14 15 b r r 0 a 6 5 26 5 8 5 + = = 2 4 2 ) 0 c x x ) 4 33 27 0 d y y ( ) = ) 15 x 36 f x + = 4 2 2 ) 10 16 e x x x
PRACTICE: SOLVEFORTHE ROOTS + + + + = 2 = 2 ) 8 14 14 )( 6 )( 6 15 1 20 0 = = = b r r r r r r ) 72 11 6 0 a c c 2 20 0 0 3 8 9 c c ( r ) ) 2 c ( 8 8 20 0 r + )( c 27 )( 3 9 16 c ( )( ) = + 0 ( ( ) 5 2r 4r 3 = 8c + = 2 3 9c + ) r + = r = 8 2 0 c or 2 5 0 4 3 0 5 3 4 c+ = 2 9 c = 8 c = or 9 2 0 8 3 0 = r = r 2 3 3 8 = c c =
MORE PRACTICE: SOLVEFORTHE ROOTS 6 26 8 ) 0 5 5 5 ( 3 1 4 5 + = = 2 4 2 c x x ) ( 4 33 )( 27 ) = + 0 d y y + )( 2 2 4 3 9 0 ) y y 2 ) + = 2 3 0 x x ( )( + = 2 4 3 3 3 0 y y y 2 5 x = ( )( ) x = 3 1 4 0 x y = y = 3 3 y = 2 y = y = N A 2 4 3 x = or 4 0 3 1 0 3 4 1 3 x = 4 x = 3 4 /
EVEN MORE PRACTICE: SOLVE ) 10 16 a x x + = 4 2x + 12 + = ( )( ) 6 2 0 x x = ( ) 2 4 2 4 2 = = x )( x 2x ) 15 b x 36 36 36 + x x 15 + 15 = ( = x 8x 2 0 0 x 2 0 x ) 0 12 3 x x x = x = 6 x = 0 6 2 0 x = 12 x = x = 12 x = 0 x = 3 0 3 2
APPLICATIONSOF QUADRATIC FUNCTIONS: Product means multiply Consecutive the terms increase by one , x x + Area of a rectangle means you multiply the length and width Two sticks have a length of 20, if one of them have a length of x , the other will have a length of 20 The difference of two numbers is 6 & x x + Sum of their squares square each number and then add them 2 & x + 1, 2 x x 6 2 y
EXAMPLE 4: THEDIFFERENCEOFTWONUMBERSIS 4. THESUMOFTHEIRSQUARESIS 136. FINDTHENUMBERS: Let x be the first number ( ) x x+ x + x + 2 2 x + 2 x + ( 10 x + 10 x = Let x + 4 be the Second number +( ) + x x 2 2 = 136 16 120 60 ) 6 x = 4 x x 4 )( = = = = 6 2 136 0 0 0 8 8 2 The you 2 possible answers for x If the first number is 10, the second number is 6 If the first number is 6, the second number is 10
EXAMPLE 5:THEWIDTHOFARECTANGLEIS 11 CM. LESS THAN 3 TIMESTHELENGTH. IFTHEAREAIS 42 SQUARE CM. FINDTHEDIMENSIONSOFTHERECTANGLE. Let the length of the rectangle be x and y be the width. That means the length is 6 cm. And therefore, the with is = = = 3 xy x 3 = 3 = ( = 11 y A A 42 0 0 x ( ) 6 cm ( ) y = y 3 7 11 3 x 2 11 11 11 )( 7 x = 2 x x + 42 6 x 3 x The dimensions are 6 cm 7cm. ) x 7 3 x = x = 6 or
A 32MTALLTREEISBROKENDURINGASEVERE STORM. THEDISTANCEFROMTHEBASEOFTHETREE TOTHETIPWHEREITTOUCHESTHEGROUNDIS 16M. ATWHATHEIGHTDIDTHETREEBREAK? ( 32 1024 1024 768 12 ) 2 + + = = = 2 2 16 16 256 64 64 32 x x x 64 + 2 2 2 2 x x 64x 256 x = x = x = 32m 32 x x The tree broke at a height of 12m 16m