Solving Quadratic Inequalities Lesson Plan

A Detailed Lesson Plan in Mathematics IV Solving Quadratic Inequalities

I. Objectives At the end of the lesson, the students should be able to: demonstrate the ability to solve quadratic inequalities using the graphic and algebraic method. internalize the concept of solving problems in different methods. correctly solve quadratic inequalities.

II. Subject Matter Topic: Solving Quadratic Inequlities References: Stewart,J., Redlin L., & Watson, S. (2007). Algebra and Trigonometry. Pasig City: Cengage Learning. pp. 122-124 http://www.regentsprep.org/Regents/math/algtrig/ ATE6/Quadinequal.htm Materials: graphing board

III. Learning Activities Teacher s Activity Student s Activity Expected response from students: A. Preparation Daily Routine Let us pray first. Good morning class! Before you take your seat, please pick up the pieces of paper under your chair. Thank you class. You may now take your seat. Let me have your attendance. Say present if you are here. (One student will lead the prayer) Good morning ma am/sir! (Students will pick up the pieces of paper.) (Students will be sitting down.) (Students will say present as the teacher calls their name.)

2. Review Before we proceed to our next topic let us first have a quick review of our previous lesson. So, what was our previous lesson all about? Very good. What do we need to know in order to solve linear inequalities? That s right. So, what are these three properties that we have discussed? Give one. Another property? Our previous lesson is all about solving linear inequalities. We need to know the rules for inequalities in order to solve linear inequalities. Addition Property of Inequality Subtraction Property of Inequality Multiplication property of Inequality Very good! And the last one?

3. Motivation PRIMING ACTIVITY

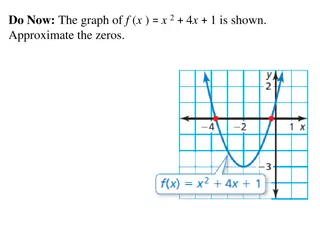
B. Presentation 1. Activity Class, could you please graph x2+ 5x 6 0 on your notebook. Who would like to share their work on the board? Thank you. That s correct. (Students perform the activity.) (One student will draw the graph on the board.)

2. Analysis Class, what do you think is the difference when we solved x2+ 5x 6 0 and x2+ 5x 6 = 0? When we have x2+ 5x 6 = 0, we will be only solving when the equation is equal to 0. When we have x2+ 5x 6 0, we will be solving for the values of x when it is equal to 0 and when it is less than 0 like -1, -2 and so on. Very good observation.

3. Abstraction Quadratic inequalities can be solved either by the use of the graphic or the algebraic method. Using the graphic method, let us solve for x2+ 5x 6 0. Let us use the graph drawn in the board. (Students will listen attentively.)

Each point on the x-axis has a y-axis Here are the steps in solving the quadratic inequalities graphically: 1. Change the inequality sign to equal sign. 2. Graph the equation. 3. From the graph, pick a number from each interval and test it in the original inequality. If the result is true, that interval is a solution to the inequality. For example based from our graph:

So the answer is x 1 and x -6 or {x -6 x 1}. Let us shade the answers. Take note that when it is or , we use close dot ( ) in plotting points but when it is < or >, we use open dot ( ) and broken line to indicate that they are not included as the answer. Now let us use the algebraic method to solve the same inequality x2+ 5x 6 0. x2+ 5x 6 0 (x 1)(x + 6) 0 Factor

Now, there are two ways this product could be less than zero or equal to 0 (x - 1) 0 and (x + 6) 0 or (x - 1) 0 and (x + 6) 0. First situation: 1. (x - 1) 0 and (x + 6) 0 x 1 and x -6 This tells us that -6 x 1.

Second situation: (x - 1) 0 and (x + 6) 0 x 1 and x -6 This tells us that 1 x -6. There are NO values for which this situation is true. Final answer: x 1 and x -6 or {x -6 x 1}. Using either the graphic or the algebraic method, we arrive at the same answer. The graph of a quadratic inequality will include either the region inside the boundary or outside the boundary. The boundary itself may or may not be included. Is it clear? Do you have any questions? Yes ma am/sir. No

4. Application Use the graphic and algebraic method to solve x2+ 8x > -15. Who wants to show their answer on the board? Very good. Can you please explain your answer? (Students will solve the inequality.) (One student will answer on the board.) (The student will explain his/her answer.)

IV. Evaluation Solve the quadratic inequality. Use both the algebraic and graphic method. 1. x2 5x + 6 0 2. x2 3x 18 0 3. 2x2+ x 1 4. x2 x 12 > 0

V. Assignment Solve the following quadratic inequality by graphic method. 1. x2+ 4 0 2. x2 4 0 Note: Graph the two quadratic inequalities in one Cartesian plane. Shade your solution. Use different colors in shading the answer in the two quadratic inequalities.