Spectroscopic Selection Rules in Transition Metal Complexes
Spectroscopic selection rules govern the intensity and allowed transitions in transition metal complexes, impacting their color and electronic behavior. The Laporte and Spin selection rules play crucial roles, determining the brightness of colors and spin changes during electronic transitions. Vibrational-electronic coupling can relax selection rules, leading to unique properties in these complexes. Theoretical paramagnetic moments reflect the interplay of spin and orbital contributions in the presence of ligand fields.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
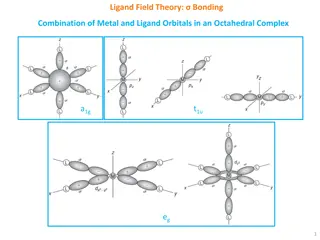
Selection Rules Some transitions are not allowed does not mean that such a transition will never occur, but that it is less likely and that the intensity (molar absorption coefficient) of such an absorption band is very low. Whether transitions are allowed or forbidden, and to what degree they may be forbidden depends on selection rules: Laporte Selection Rule: In a molecule having center of symmetry, transitions between states of the same parity (symmetry with respect to a center of inversion) are forbidden. For example, transitions between states that arise from dorbitals are forbidden (g g transitions; d orbitals are symmetric to inversion), but transitions between states arising from d and p orbitals are allowed (g u transitions; p orbitals are anti- symmetric to inversion). Therefore, all d-d transitions in octahedral complexes are Laporte-forbidden. Laporte-allowed transitions involve l = 1. f etc allowed ( l = 1) s p , p d , d f etc forbidden ( l = 2) s d , p s s , p p , d d , f f etc forbidden ( l = 0) 1
Relaxation of Laporte Selection Rule Like all chemical bonds, octahedral complexes vibrate in ways (unsymmetrical vibrations) in which the center of symmetry is temporarily lost. This phenomenon, called vibronic (vibrational-electronic) coupling, can relax Laporte selection rule. They are often responsible for the bright colors of these complexes. In tetrahedral complexes, there is no center of symmetry and thus orbitals have no g or u designation. Therefore, the Laporte rule does not apply and the complexes exhibit strong colors. Intensities of Spectroscopic Bands in 3d Complexes max (L mol-1 cm-1) 10-3-1 Band Type Spin forbidden, Laporte forbidden Spin allowed, Laporte forbidden 1-100 Spin allowed, Laporte allowed 100-1000 1,000-106 Symmetry allowed (charge-transfer bands) 2
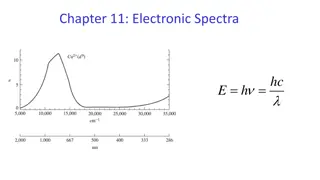
Selection Rules Spin Selection Rule: The overall spin S of a complex must not change during an electronic transition, hence, S = 0. To be allowed, a transition must involve no change in spin state. This is because electromagnetic radiation usually cannot change the relative orientation of an electron spin. [Mn(H2O)6]2+ has a d5configuration and it is a high-spin complex. Electronic transitions are not only Laporte-forbidden, but also spin-forbidden. The dilute solutions of Mn2+ complexes are therefore colorless. Certain complexes like MnO4- and CrO42- are intensely colored even though they have metal ions without electrons in d orbitals. The color of these complexes are not from d-d transitions, but from charge-transfer from ligand to metal orbitals. 3
Theoretical Paramagnetic Moment Paramagnetic moment originates from spin and orbital motion of unpaired electrons. When there is significant spin and orbital angular momentum contributions, theoretical is given by: S+L The observed value of in complexes is always less than the theoretical value calculated from above equation. This occurs because the ligand field quenches orbital contribution to some extent. In the extreme case when L = 0, the orbital contribution to the magnetic moment is said to be quenched. When orbital angular momentum is absent, theoretical is given by: s.o. S = n/2 gives spin-only formula: s.o. 4
Orbital contribution to Magnetic Moment All values are for high-spin octahedral complexes. 5
When does orbital angular momentum contribute to paramagnetic moment? For orbital angular momentum to contribute, there must be an equivalent and degenerate orbital (similar in energy to that of the orbital occupied by the unpaired electrons). If this is so, the electrons can make use of the available orbitals to circulate or move around the center of the complexes and hence generate L and L (it is the rotation of the electrons which induces the orbital contribution). Essential Conditions: 1) The orbitals should be degenerate (t2g or eg). 2) The orbitals should be similar in shape and size, so that they are transferable into one another by rotation about the same axis. 3) Orbitals must not contain electrons of identical spin. 6
When does orbital angular momentum contribute to paramagnetic moment? For an octahedral complex: Condition t2g set 1 eg set Obeyed Obeyed 2 Obeyed Not obeyed 3 Since condition 1 and 2 are satisfied, condition 3 will dictate whether it will generate l or not. Does not matter since condition 2 is already not obeyed. These conditions are fulfilled whenever one or two of the three t2g orbitals contain an odd number of electrons. For an octahedral complex, orbital contributions are possible only when the t2g orbitals are asymmetrically occupied and for a tetrahedral complex, the t2 orbitals have to be asymmetrically occupied. 7
When does orbital angular momentum contribute to paramagnetic moment? 90o rotation about z-axis 45o rotation about z-axis dxy orbital can be converted into dx2-y2 orbital by a 45 rotation about z-axis. But, in an octahedral crystal field, the degeneracy between the dxy and dx2-y2 orbitals is lifted. Hence, orbital contribution about z-axis from dxy, dx2-y2 pair of orbitals disappears. dx2-y2 and dz2 orbitals can not be interconverted by rotation due to their different shapes. Thus, e(g) electrons have no orbital contribution to magnetic moment. 8
When does orbital angular momentum contribute to paramagnetic moment? dxz orbital can be converted into dyz orbital by a 90 rotation about z-axis. Thus, all t2(g) orbitals may be interconverted by rotation about suitable axes and we may expect orbital contributions from t2(g) electrons. If all the t2g orbitals are singly occupied (t2g3), an electron in, say, dxz orbital cannot be transferred into dyz orbital because it already contains an electron having the same spin quantum number as the incoming electron; if all the t2g orbitals are doubly occupied (t2g6), the transfer is not possible. Thus, only configurations other than t2g3 and t2g6 make orbital contributions to magnetic moments. For high-spin octahedral complexes, orbital contribution is expected for: t2g1, t2g2, t2g4eg2 and t2g5eg2. For tetrahedral complexes, orbital contribution is expected for: e2t21, e2t22, e4t24 and e4t25. 9