Statistics Summary for Data Set Analysis
This summary presents key statistics for a dataset, including the minimum and maximum values, range, average, median, standard deviation, and variance. The data provides insights into the distribution and central tendencies of the values, aiding in understanding the overall pattern and variability within the dataset.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
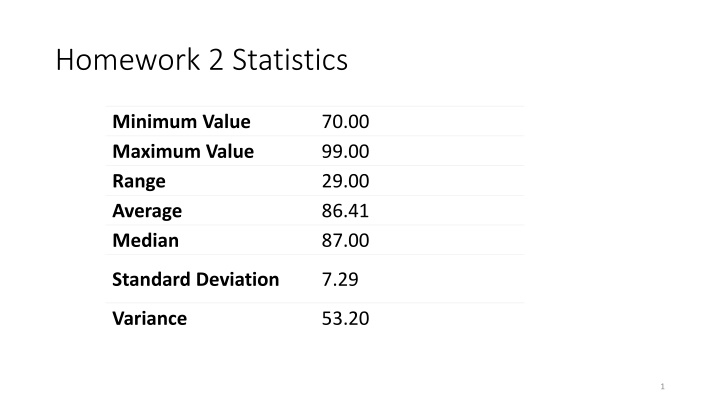
Homework 2 Statistics Minimum Value Maximum Value Range Average Median 70.00 99.00 29.00 86.41 87.00 Standard Deviation 7.29 Variance 53.20 1
Midterm Exam Date: Tuesday, October 16th Time: 3PM-4:15PM (in class) Location: Lawson B134 (right here) Closed Book/No Calculator Note: Our TA (Duc Le) will proctor the midterm Content: Includes today s lecture (chapters 1-7) Preparation: You may prepare one 3x5 inch index card (double sides). Take the practice final Review homework solutions, book, lecture notes etc. 2
Final Exam (Tentative) Date: Tuesday, December 11th (Subject to Change*) Time: 8AM (Subject to Change*) Location: LWSN B151 (Subject to Change*) * Purdue will not reimburse you for flight re-booking fees 3
Cryptography CS 555 Week 8: One-Way Functions (Part 2) Fall 2018 4
Recap Corollary: If one-way functions exist then PRGs, PRFs and strong PRPs all exist. Corollary: If one-way functions exist then there exist CCA- secure encryption schemes and secure MACs. We saw how to build PRGs from One-Way- Permutations 5
n-bits n-bits PRFs from PRGs G(x):= G0(x) || G1(x) Theorem: Suppose that there is a PRG G with expansion factor ? = 2?. Then there is a secure PRF. 1 Fk(011)=G1(G1(G0(k))) 0 k G0(k) G1(k) 0 1 1 0 G1(G1(k)) G0(G0(k)) G0(G1(k)) G1(G0(k)) 1 1 0 0 1 1 0 0 6
PRFs from PRGs Theorem: Suppose that there is a PRG G with expansion factor ? = 2?. Then there is a secure PRF. Proof: Proof: Claim 1: For any t(n) and any PPT attacker A we have Claim 1: For any t(n) and any PPT attacker A we have ?? ? ?? ??(?) ?? ? ? ?? ? ??(?) < ????(?) 7
PRFs from PRGs Claim 1: For any t(n) and any PPT attacker A we have Claim 1: For any t(n) and any PPT attacker A we have ?? ? ?? ??(?) ?? ? ? ?? ? ??(?) < ???? ? Proof Sketch (by Triangle Inequality): Fix Proof Sketch (by Triangle Inequality): Fix j j ???? = ?? ? ?? ??+? ? ??+? ? ??(?) ?? ? ?? ?? ? ??+? ? ??(?) This difference is negligible by PRG security (just replaced This difference is negligible by PRG security (just replaced ? ??+? ???? ??+?). < ???? ? 8
PRFs from PRGs Claim 1: For any t(n) and any PPT attacker A we have Claim 1: For any t(n) and any PPT attacker A we have ?? ? ?? ??(?) ?? ? ? ?? ? ??(?) < ???? ? Proof Sketch ?? ? ?? ??(?) ?? ? ? ?? ? ??(?) ???? ?<? ? ? ? ???? ? = ???? ? (???) 9
Hybrid H0 (Real Construction) n-bits n-bits G(x):= G0(x) || G1(x) 1 Fk(011)=G1(G1(G0(k))) 0 k G0(k) G1(k) 0 1 1 0 G1(G1(k)) G0(G0(k)) G0(G1(k)) G1(G0(k)) 1 1 0 0 1 1 0 0 10
Hybrid H1 (Real Construction) n-bits n-bits G(x):= G0(x) || G1(x) 1 0 Fk(011)=G1(G1(r0)) k r0 r1 0 1 1 0 G1(G1(k)) G0(G0(k)) G0(G1(k)) G1(G0(k)) 1 1 0 0 1 1 0 0 11
Hybrid H2 n-bits n-bits G(x):= G0(x) || G1(x) 1 0 r Fk(011)=G1(r01) r0 r1 0 1 1 0 r11 r00 r10 r01 1 1 0 0 1 1 0 0 12 12
Hybrid Hn (truly random function!) n-bits n-bits G(x):= G0(x) || G1(x) 1 0 r Fk(011)=r011 r0 r1 0 1 1 0 r11 r00 r10 r01 1 1 0 0 1 1 0 0 r000 r001 r110 r111 r010 r011 r100 r101 13 13
Hybrid H1 vs H2 Claim 1: For any t(n) and any PPT attacker A we have Claim 1: For any t(n) and any PPT attacker A we have ?? ? ?? ??(?) ?? ? ? ?? ? ??(?) < ???? ? Claim 2: Claim 2: Attacker who makes t(n) oracle queries to our function cannot Attacker who makes t(n) oracle queries to our function cannot distinguish H distinguish Hi i from H from Hi+1 (except with negligible probability). i+1 (except with negligible probability). Proof: Indistinguishability follows by Claim 1 Proof: Indistinguishability follows by Claim 1 Let x Let x1 1, , x xt t denote the t queries. Let y denote the t queries. Let y1 1, , query. query. ( (H Hi+1 vs H Hi i : replaced : replaced ? ??? with , ,y yt t denote first denote first i i bits of each bits of each i+1 vs with ??? ? ??? ?) ) 14
Hybrid H2 vs H1 G(r0) vs. r00 ||r01 n-bits n-bits G(x):= G0(x) || G1(x) Irrelevant: (Unexplored) 1 0 r r0 r1 0 1 1 0 r11 r00 r10 r01 1 1 0 0 1 1 0 0 15 x x1 1 x x2 2 x xt t 15
Triangle Inequality Claim 1: For any t(n) and any PPT attacker A we have Claim 1: For any t(n) and any PPT attacker A we have ?? ? ?? ??(?) ?? ? ? ?? ? ??(?) < ???? ? Claim 2: Claim 2: Attacker who makes t(n) oracle queries to our function cannot Attacker who makes t(n) oracle queries to our function cannot distinguish H distinguish Hi i from H from Hi+1 (except with negligible probability). i+1 (except with negligible probability). Triangle Inequality: Attacker cannot distinguish Triangle Inequality: Attacker cannot distinguish F Fk k ( (H H0 0) from f ( ) from f (H Hn n). ). 16
From OWFs (Recap) Theorem: Suppose that there is a PRG G with expansion factor ? = ? + 1. Then for any polynomial p(.) there is a PRG with expansion factor p(n). Theorem: Suppose that there is a PRG G with expansion factor ? = 2?. Then there is a secure PRF. Theorem: Suppose that there is a secure PRF then there is a strong pseudorandom permutation. 17
From OWFs (Recap) Corollary: If one-way functions exist then PRGs, PRFs and strong PRPs all exist. Corollary: If one-way functions exist then there exist CCA- secure encryption schemes and secure MACs. 18
Are OWFs Necessary for Private Key Crypto Previous results show that OWFs are sufficient. Can we build Private Key Crypto from weaker assumptions? Short Answer: No, OWFs are also necessary for most private-key crypto primitives 19
PRGs OWFs Proposition 7.28: If PRGs exist then so do OWFs. Proof: Let G be a secure PRG with expansion factor ? = 2?. Question: why can we assume that we have an PRG with expansion 2n? Answer: Last class we showed that a PRG with expansion factor ? = ? + 1. Implies the existence of a PRG with expansion p(n) for any polynomial. 20
PRGs OWFs Proposition 7.28: If PRGs exist then so do OWFs. Proof: Let G be a secure PRG with expansion factor ? = 2?. Claim: G is also a OWF! (Easy to Compute?) (Hard to Invert?) Intuition: If we can invert G(x) then we can distinguish G(x) from a random string. 21
PRGs OWFs Proposition 7.28: If PRGs exist then so do OWFs. Proof: Let G be a secure PRG with expansion factor ? = 2?. Claim 1: Any PPT A, given G(s), cannot find s except with negligible probability. Reduction: Assume (for contradiction) that A can invert G(s) with non- negligible probability p(n). Distinguisher D(y): Simulate A(y) Output 1 if and only if A(y) outputs x s.t. G(x)=y. 22
PRGs OWFs Proposition 7.28: If PRGs exist then so do OWFs. Proof: Let G be a secure PRG with expansion factor ? = 2?. Claim 1: Any PPT A, given G(s), cannot find s except with negligible probability. Intuition for Reduction: If we can find x s.t. G(x)=y then y is not random. Fact: Select a random 2n bit string y. Then (whp) there does not exist x such that G(x)=y. Why not? 23
PRGs OWFs Proposition 7.28: If PRGs exist then so do OWFs. Proof: Let G be a secure PRG with expansion factor ? = 2?. Claim 1: Any PPT A, given G(s), cannot find s except with negligible probability. Intuition: If we can invert G(x) then we can distinguish G(x) from a random string. Fact: Select a random 2n bit string y. Then (whp) there does not exist x such that G(x)=y. Why not? Simple counting argument, 22npossible y s and 2nx s. Probability there exists such an x is at most 2-n (for a random y) 24
What other assumptions imply OWFs? PRGs OWFs (Easy Extension) PRFs PRGs OWFs Does secure crypto scheme imply OWFs? CCA-secure? (Strongest) CPA-Secure? (Weaker) EAV-secure? (Weakest) As long as the plaintext is longer than the secret key Perfect Secrecy? X (Guarantee is information theoretic) 25
EAV-Secure Crypto OWFs Proposition 7.29: If there exists a EAV-secure private-key encryption scheme that encrypts messages twice as long as its key, then a one-way function exists. Recap: EAV-secure. Attacker picks two plaintexts m0,m1 and is given c=EncK(mb) for random bit b. Attacker attempts to guess b. No ability to request additional encryptions (chosen-plaintext attacks) In fact, no ability to observe any additional encryptions 26
EAV-Secure Crypto OWFs Proposition 7.29: If there exists a EAV-secure private-key encryption scheme that encrypts messages twice as long as its key, then a one-way function exists. Reduction: ? ?,?,? = ?????;? ?. Input: 4n bits (For simplicity assume that Enck accepts n bits of randomness) Claim: f is a OWF 27
EAV-Secure Crypto OWFs Proposition 7.29: If there exists a EAV-secure private-key encryption scheme that encrypts messages twice as long as its key, then a one-way function exists. Reduction: ? ?,?,? = ?????;? ?. Claim: f is a OWF Reduction: If attacker A can invert f, then attacker A can break EAV- security as follows. Given c=Enck(mb;r) run A(c ?0). If A outputs (m ,k ,r ) such that f(m ,k ,r ) = c ?0 then output 0; otherwise 1; 28
MACs OWFs In particular, given a MAC that satisfies MAC security (Definition 4.2) against an attacker who sees an arbitrary (polynomial) number of message/tag pairs. Conclusions: OWFs are necessary and sufficient for all (non-trivial) private key cryptography. OWFs are a minimal assumption for private-key crypto. Public Key Crypto/Hashing? OWFs are known to be necessary Not known (or believed) to be sufficient. 29
Computational Indistinguishability Consider two distributions X and Y (e.g., over strings of length ). Let D be a distinguisher that attempts to guess whether a string s came from distribution X or Y . The advantage of a distinguisher D is ????, = ??? X ? ? = 1 ??? Y ? ? = 1 Definition: We say that an ensemble of distributions ?? ? and ?? ? are computationally indistinguishable if for all PPT distinguishers D, there is a negligible function negl(n), such that we have ????,? ????(?) 30
Computational Indistinguishability The advantage of a distinguisher D is ????, = ??? X ? ? = 1 ??? Y ? ? = 1 Looks similar to definition of PRGs Xn is distribution G(Un) and Yn is uniform distribution ? (n) over strings of length (n). 31
Computational Indistinguishability Definition: We say that an ensemble of distributions ?? ? and ?? ? are computationally indistinguishable if for all PPT distinguishers D, there is a negligible function negl(n), such that we have ????,? ????(?) ?(?) and ??= Theorem 7.32: Let t(n) be a polynomial and let ??= ?? ?? indistinguishable ?(?)then the ensembles ?? ? and ?? ? are computationally 32
Computational Indistinguishability Definition: We say that an ensemble of distributions ?? ? and ?? ? are computationally indistinguishable if for all PPT distinguishers D, there is a negligible function negl(n), such that we have ????,? ????(?) Fact: Let ?? ? and ?? ? be computationally indistinguishable and let ?? ? and ?? ? be computationally indistinguishable Then ?? ? and ?? ? are computationally indistinguishable 33
Practice Problems Suppose that f is a OWF. Build another OWF f s.t. f is not collision resistant. Suppose that hs(.) is collision resistant hash function mapping 2n-bit strings to n-bit strings. Show that f(s,x)= (s,hs(x)) is a one-way function. Suppose that hs(.) is collision resistant hash function mapping 2n-bit strings to n-bit strings. Show that f(s,x)= hs(x) is not necessarily a OWF. ? ?,?,? = ?????;? ? is a OWF. What about ? ?,?,? = ?????;? ? Is it necessarily One-Way? 34