Stochastic Games: Understanding Expectiminimax in Artificial Intelligence
Stochastic games, like backgammon, involve randomness and a mix of luck and skill. Learn about chance nodes, expectiminimax value calculation, game trees, and evaluation functions in AI.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
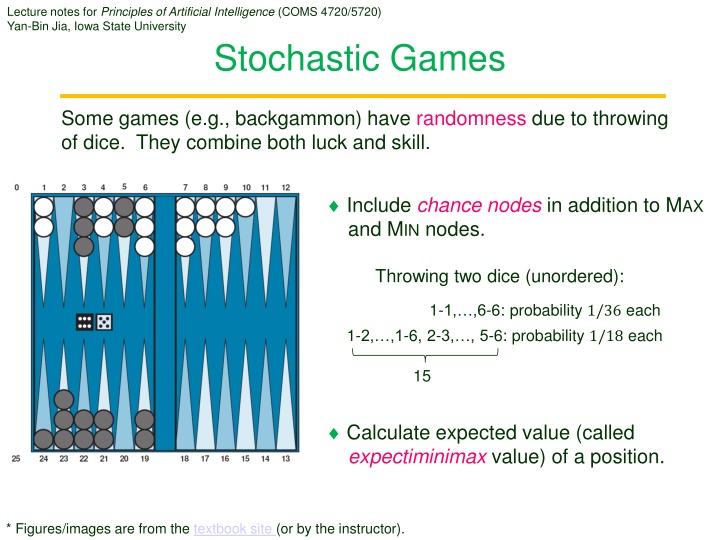
Lecture notes for Principles of Artificial Intelligence (COMS 4720/5720) Yan-Bin Jia, Iowa State University Stochastic Games Some games (e.g., backgammon) have randomness due to throwing of dice. They combine both luck and skill. Include chance nodes in addition to MAX and MIN nodes. Throwing two dice (unordered): 1-1, ,6-6: probability 1/36 each 1-2, ,1-6, 2-3, , 5-6: probability 1/18 each 15 Calculate expected value (called expectiminimax value) of a position. * Figures/images are from the textbook site (or by the instructor).
Game Tree for a Backgammon Position 1. MAX chooses an action, say, ?3 out of ?1,..,?? and executes it. 2. MIN rolls a die and gets a set of legal actions ?1,..,?? under some CHANCE node. 3. MIN chooses an action, say, ?1, from the set and executes it. 4. MAX rolls a die and gets a set of legal actions. 5. Repeat steps 1-4 until a terminal state is reached. ?? ?1 ?3 ?2 (a dice roll) probability 1st set of legal moves for MIN ?? ?1 ?2
Expectiminimax Value EXPECTIMINIMAX(?) = UTILITY(?, MAX) if Is-TERMINAL(?) max ?EXPECTIMINIMAX(RESULT(?,?))if TO-MOVE(?) = MAX min ?EXPECTIMINIMAX(RESULT(?,?))if TO-MOVE(?) = MIN ??(?)EXPECTIMINIMAX(RESULT(?,?))if TO-MOVE(?) = CHANCE expected value one possible dice roll
Evaluation Functions Evaluation functions with the same order of leaf values can yield different move choices at a state. Best move Best move Alpha-beta pruning is still applicable if we can bound values on chance nodes.