Strain and Stress Analysis: Pendulum Impact Test and Steel Plate Elongation
Explore the detailed analysis of strain and stress in materials through a pendulum impact test and determination of elongation in a steel plate under axial force. Understand lateral strain and Poisson's ratio effects under different stress conditions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
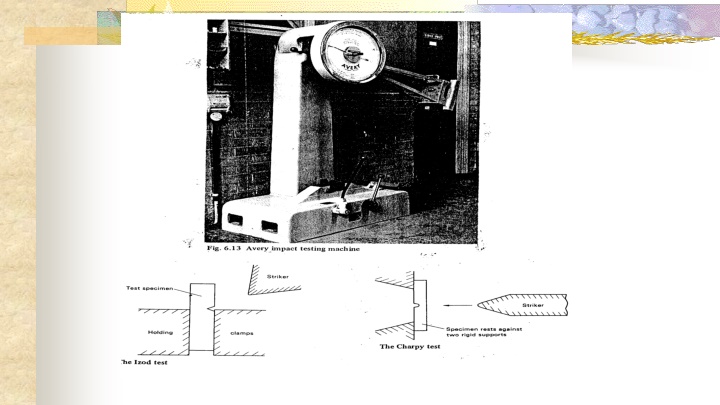
Impact Test Concluded The difference in height from which a pendulum is released and the height to which it rises after measure of the energy absorbed by the specimen and this is recorded on a dial mounted on a tester. impact gives a
A flat plate of steel, 1 cm thick, and of trapezoidal form tapers from 5 cm width to 10 cm width in a length of 40 cm. Determine the elongation under an axial force of 50 kN. E = 2 x 107N/cm2. Steel Diagram of a Trapezoidal l Plate t dx B1 P P B2 x L
Solution Consider a length, dx at a distance, x from width, B1, Width at that section L B B = + = + 2 1 B x B Kx 1 1 L B B = 2 1 where K Area (Ax) of chosen c/section = ( B1 + K x ) t. If the length dx elongates an amount du under load, its strain is: .1 du dx P A E =
Solution Contd. Total extension of bar, u z z z P P Kx t E ) L L = = u dx dx + A E x ( B 0 0 1 P dx + P L 0 L = = + u ln B Kx 1 t E B kx + KtE 0 1 B K L P = 1 u ln K t E B 1
Solution Contd. Substituting back for K, + B B B B P B = 1 2 1 u ln B 2 1 ( ) t E 1 L B B P B = 2 u ln B 2 1 ( ) t E 1 L In problem, t = 1 cm, B1 = 5 cm, B2 = 10 cm, L = 40 cm, P = 50,000 N, E = 2 x 107 N/cm2 50 000 , N 10 5 = = u ln 001386 . cm 10 5 40 7 ( ) x cm x 1 2 10 x
Solution Concluded Substituting back for K, + B B B B P B = 1 2 1 u ln B 2 1 ( ) t E 1 L B B P B = 2 u ln B 2 1 ( ) t E 1 L In problem, t = 1 cm, B1 = 5 cm, B2 = 10 cm, L = 40 cm, P = 50,000 N, E = 2 x 107 N/cm2 50 000 , N 10 5 = = u ln 001386 . cm 10 5 40 7 ( ) x cm x 1 2 10 x
1.9 Lateral Strain and Poissons Ratio Under the action of a longitudinal stress, a body will extend in the direction of the stress and contract in the transverse or lateral direction (see Fig. below). The reverse occurs under a compressive load.
Stress Effects P P Longitudinal Tensile Stress Effect P P Longitudinal Compressive Stress Effect
