Surds Multiplication and Rationalisation Techniques
Learn about surds multiplication, rationalisation, and solving equations using index and surd rules. Practice various exercises to enhance your understanding.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
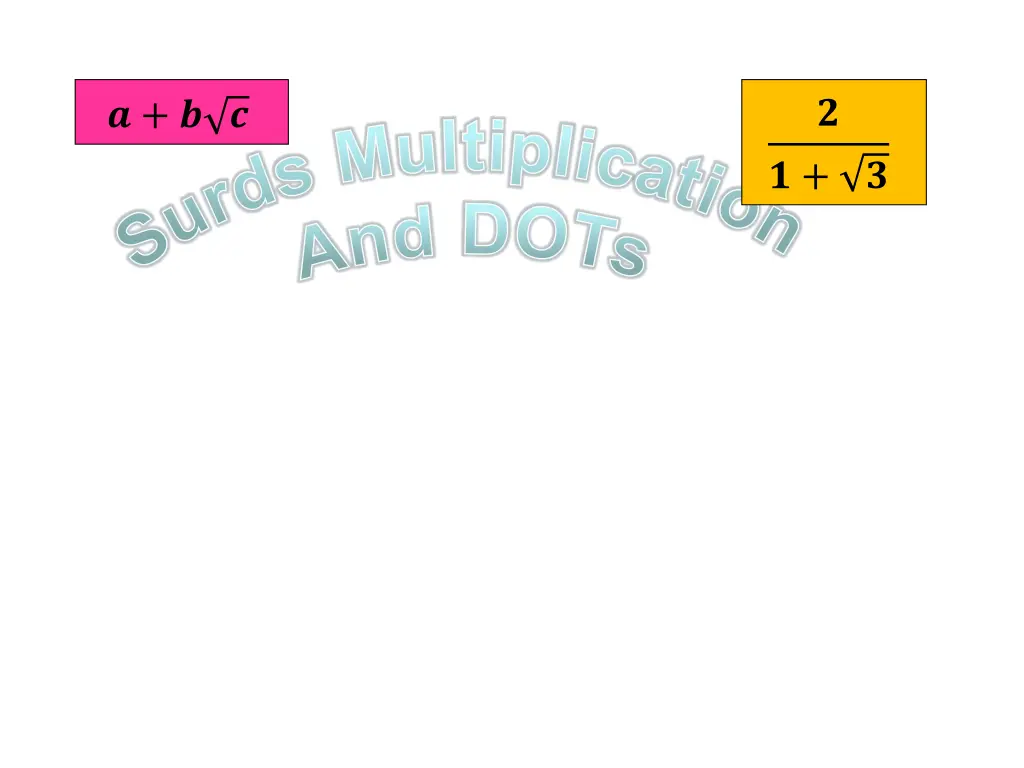
? ? + ? ? Surds Multiplication And DOTs ? + ?
Surds Multiplication BAT simplify and rationalise surds BAT solve equations using the rules for indices and surds KUS objectives Starter: ?? ?? ? ? ? ?? ? ?? ? 5 ? ? ? ?
WB29a Explore making an integer Multiply each of the given numbers by a single term to give an integer answer 3 2 5 2 7 3 + 2
WB29b making an integer (2 + 3) (2 - 3) Multiply by the conjugate = 4 - 2 3 + 2 3 - 3 3 = 4 + 0 - 3 = 1 This is the same structure as difference of squares for quadratics (1 + 5)(1 - 5) Now try these: (6 + 2 3)(6 - 2 3)
Practice 1: Rationalise these! 3 1 + 3 1 + 2 3 7 4 + 7 5 + 3 7 5 1 5 2 5 + 2 2 3 3 + 4 3 3 - 6 5 6 2 - 7 2 7- 3 10 5 10 4 7 - 3 5
Summary Notes: Rationalise a surd This is a trick to make the denominator an integer when you have a surd as a denominator. First make sure you are happy that a a = a (a + b)(a - b) = a2 b2 and 11 11 = 11 (7 + 11) (7 - 11) = 49 11 11 = 49 11 = 38
KUS objectives BAT simplify and rationalise surds BAT solve equations using the rules for indices and surds self-assess One thing learned is One thing to improve is