Surface Tension in Solid-Vapor Interface

Chap. 17.8(a) Solid-Vapor Interface => Surface Tension ( Interface) -A molecule in the bulk has a lower potential energy than one free in the gas (below the transition temperature). - When a molecule is at the surface, its energy is intermediate between free molecule and the molecule in the bulk. - Its potential energy would be lowered if it moved into the bulk, and so the molecules are under the influence of a force, which tends to draw them into the bulk. - This force is attractive reducing total surface area, and we term it a tension, the surface tension. Solid-Vapor Interface Solid Microscopic basis of surface tension. Vapor Dangling Bonds force inwards tends to contract the surface, i.e. there is a surface tension Force relatively high potential energy (bulk) relatively low potential energy page 1 = handwave argument 1 http://bp.snu.ac.kr

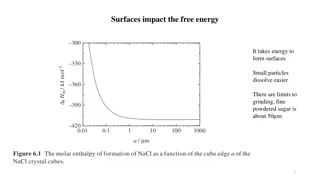
Liquids (or solids) assume a shape that minimizes their surface area because it enables the maximum number of molecules to the bulk rather than surface. The work involved in forming a surface of area dA is proportional to the area of the surface formed. dw = dA where is a coefficient known as the surface tension of the material. + = ___________ + dA dG SdT Vdp page 2 = exact At constant pressure and temperature, dA dG = : which means that surfaces have a natural tendency to contract. 0 0 dG dA Surface Tension = Interfacial Gibbs-Free Energy 2 http://bp.snu.ac.kr

(skip - - -) = Work 2 hl work = Since = the distance, the times force the is = 2 / 2 / f w h hl h l Force 2 l Total area 2hl Figure 4.21 The model used for calculating the work of forming a liquid film when a wire of length l is raised and pulls the surface with it through a height h. 3 http://bp.snu.ac.kr

(skip - - -) Consider a bubble (or cavity). Pin Pin: the pressure inside the cavity Pout: the outside pressure The internal pressure is due to the sum of the outside pressure Poutand the surface tension. The change in surface area when the radius of a sphere changes from r and r +dr is dr2is ignored = 4 ( + 2 2 ) 4 8 d r dr r rdr = = r dr 8 dw d As force distance is work, the force opposing stretching through the distance dr at this radius=8 r 4 http://bp.snu.ac.kr

(skip - - -) = + 2 2 4 4 8 r p r p r in out 2 = Laplace equation p p in out r Note: The Laplace equation shows that the pressure inside a curved surface is always greater than the pressure outside, but the difference decreases to zero as the radius of curvature becomes infinite. 5 http://bp.snu.ac.kr

Pressure inside, pin 2 = r p p in out r Increasing surface tension, Figure 4.22 The dependence of the pressure inside a curved surface on the radius of the surface, for two different values of the surface tension. pout Radius, r 6 http://bp.snu.ac.kr

Consider droplets. At equilibrium, the chemical potentials of a vapor and its liquid are equal. ( ) ( ) d g d l = Let the pressure on the system be increased. If the pressure on the liquid changes by dp(l), then the change in the presence of its pressure, dp(g) will be such that = ( ) ( ) ( ) ( ) V g dp g V l dp l T ( at const ant ) m m = V dp S dT = d d V dp at const ant pr essur e m m m RT = Assuming that the vapor is ideal, ( ) g . V m ( ) p g ( ) RT ( ) ( ) ( ) p g V l dp l RT dp g = = ( ) ( ) ( ) dp g V l dp l m m ( ) p g 7 http://bp.snu.ac.kr

On integration with boundary condition of p*(g)=p*(l), when the pressure exerted on the liquid is the normal pressure p*, i.e., p(g)=p* and p(l)=p*, + * p p p ( ) ( ) p g 1 dp g = ( ) ( ) V l dp l m RT * * p p V RT V p V p p ( ) = + = = * ln * * exp p p p p p m m RT m RT * p One way of increasing the pressure on the liquid is to disperse it as droplets. The pressure differential across a curved surface is 2 /r. 2 = ( ) ( )exp ( ) p p V l m i st bul k Kel vi n e quat i on m rRT where p(mist) is the vapor pressure of a sample of mist with droplet radius r and p(bulk) is the pressure of a plane surface of the same material. 8 http://bp.snu.ac.kr

The pressure exerted by a column = p gh : l i qui d densi t y 2 2 = + = p p gh gh r r 2 1 2 = = , h ghr gr Figure 4.23 When a capillary tube is first stood in a liquid, the latter climbs up the walls, so curving the surface. The pressure just under the meniscus is less than that arising from the atmosphere by 2g/r. The pressure is equal at equal heights throughout the liquid provided the hydrostatic pressure (which is equal to rgh) cancles the pressure difference arising from the curvature. 9 http://bp.snu.ac.kr

Surface tension, /(mN m-1) Figure 4.24 The variation of the surface tension of water with temperature. Temperature, / C 10 http://bp.snu.ac.kr

sg = + cos sg sl lg + c sg sl = cos c lg sg> sl the liquid wets (spread over) c o 0 90 sg< sl c o 90 c lg Figure 4.25 The balance of forces that results in a contact angle, c. sl 11 http://bp.snu.ac.kr

Thermodynamic work of adhesion The thermodynamic work of adhesion, wad, required to separate a unit area of a solid and a liquid phase forming an interface across which secondary forces are acting may be related to the surface and the interfacial free energies by the Dupre equation. The reversible work of adhesion, wad, in an inert medium may be expressed by: wad= (sum of the surface free energies of the solid and liquid phase the interfacial free energy) = + i.e., w (1) ad sg lg sl = + cos (2) sg sl lg c (3) sg sl = cos c lg 12 http://bp.snu.ac.kr

Combining eq (1) and eq (3) gives w = cos 1 ad (4) c lg We now see that the liquid completely wets (spreads over) the surface fully, corresponding to c 0, when wad 2 lg . The liquid does not wet the surface (corresponding to c> 90 when wad< lg). 13 http://bp.snu.ac.kr

1 cos c 0 0 1 2 wad/ lg -1 Figure 4.26 The variation of contact angle (shown by the semaphore-like object) as the ratio wad / lgchanges. 14 http://bp.snu.ac.kr