Sustainable Power Solutions for Rural Development
Save Earth by recycling bio-waste to generate electricity and fuel. Learn about bio-waste to energy flow chart and the proven sustainable power solutions offered. Discover how bio-waste can be utilized as raw material for electricity generation, benefiting industries, villagers, farmers, and institutions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
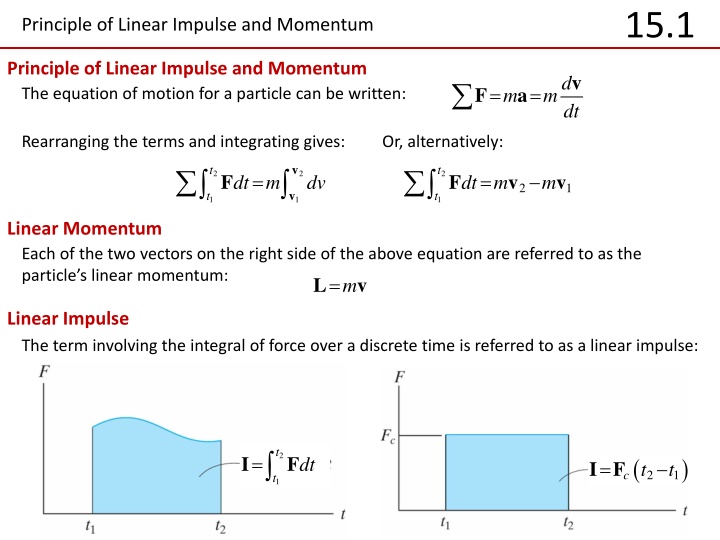
15.1 Principle of Linear Impulse and Momentum Principle of Linear Impulse and Momentum The equation of motion for a particle can be written: v d = = F a m mdt Rearranging the terms and integrating gives: Or, alternatively: v t t F 2 2 2 dt m = dt m = F v v dv m 2 1 v t t 1 1 1 Linear Momentum Each of the two vectors on the right side of the above equation are referred to as the particle s linear momentum: L = v m Linear Impulse The term involving the integral of force over a discrete time is referred to as a linear impulse: t = 2 ( ) I F dt = I F c t t 2 1 t 1
15.1 Principle of Linear Impulse and Momentum Principle of Linear Impulse and Momentum t It is often convenient to write the principle of linear impulse and momentum as: 2 + dt m = v F v 2 EQ 15-3 m 1 t 1 t 2 + F dt m v = ( ) m v ( ) The principle of linear impulse can be resolved into its x, y, z components so that: 1 2 x x x t 1 t 2 + F dt m v = ( ) ( ) EQ 15- 4 m v 1 2 y y y t 1 t 2 + F dt m v = ( ) m v ( ) The principle of linear impulse can be illustrated with the momentum and impulse diagrams: 1 2 z z z t 1
15.1 Principle of Linear Impulse and Momentum Solving Impulse and Momentum Problems Draw a FDB (or multiple FBD s for objects interacting with one another) Write the Principle of Impulse equations for each direction where there is a force acting on the object(s) Make sure to include forces between objects if that is something you are trying to calculate All of the external forces should be included in the Principle of Impulse equations, multiplied by the time the forces are acting on them
15.2 Principle of Linear Impulse and Momentum for a System of Particle Principle of Linear Impulse and Momentum for a System of Particles The principle of linear impulse can be extended to a system of particles: t ( ) v ( ) v 2 + = F 2 EQ 15-6 m dt m i i i i i 1 t 1 The location of the mass center G of the system is determined by: = r i i r m m G = v v m m Taking a time derivative gives: G i i The equation above states that the total linear momentum of the system of particles is equivalent to the linear momentum an imaginary aggregate particle moving with the velocity of the mass center of the system. Thus: t ( ) ( ) 2 + dt m = v F v m G i G 1 2 t 1
15.3 Conservation of Linear Momentum for a System of Particle Principle of Linear Impulse and Momentum for a System of Particles When the sum of the external impulses acting on a system of particles is zero, the conservation of linear momentum equation is: ( ) v ( ) v = 2 EQ 15-8 m m i i i i 1 This equation states that the total linear momentum for a system of particles remains constant during the time period from t1 to t2. = By making the substitution , , EQ 15-8 can be written: G m v v m i i ( ) ( ) = v v G G 1 2 This equation indicates that the velocity of the mass center for the system of particles does not change if no external impulses are applied to the system.
In-Class Practice Problem 1 If we only want to know final velocity, could treat as one object Since we want the force between the two objects we need to do separate FBD s for each crate Plus, this makes a great warm-up for PLIM equations
In-Class Practice Problem 1 FBD of Crate A, and Principle of Linear Impulse Equations in y and x directions
In-Class Practice Problem 1 FBD of Crate B, and Principle of Impulse Equations in y and x directions
In-Class Practice Problem 1 Two Equations, and Two Unknowns Solution:
In-Class Practice Problem 2 This problem only has motion and forces in the y-direction The special case is that for the first chunk of time the force on the cable isn t enough to move the crate. You could analyze this portion, but you would just be showing that 0 + 0 = 0. First, find the time when the cable force is able to move the crate, then apply the principle of impulse equations from that time until t = 4