The Power Curve Interpolation Issue

Understanding the Power Curve Interpolation Issue Power Curve Working Group, 2016-03-10, Hamburg Axel Albers

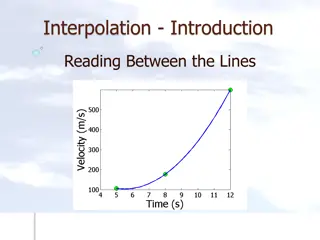
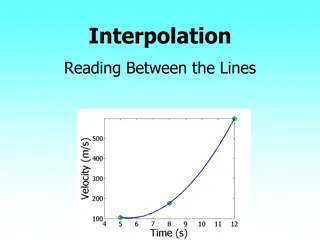
Illustration of Interpolation Problem Source: P. Stuart, PCWG meeting London Dec. 2015 Power curve raw data PActual(t) is first bin-averaged (baseline power curve in inner range) Bin averages are interpolated in order to derive power from bin-averaged power curve for actual wind speed: PBaseline(t) or PCandidate(t) 1 www.windguard.de www.windguard.de

Inner Range Baseline Error ( ) t ( ) t ( ) t = P P Baseline Baseline Actual P = Normalised Mean Error (NME) Actual Source: P. Stuart, PCWG meeting London Dec. 2015 If NME is calculated for the inner range, it is expected to be zero (inner range baseline error) But it isn t: NME positive where power curve left-curved and negative where power curve right-curved 2 www.windguard.de www.windguard.de

Explanation of Interpolation Error P ( P ( ) t ( ) t ( ) t = P P = NME Baseline Baseline Actual Actual ( ) P Actual ( ) P ( ) t ) t P Baseline Actual = NME ( ) t ( ) t P t P Baseline Actual = NME ( ) t Actual ( ) t P average bin : of P Baseline i , Baseline Baseline P Actual P i , i , = NME ( ) t i Actual P P bin : average of P i , Actual i , Actual The cause of the non-zero inner baseline error is the difference of the bin average of the power curve raw data and the bin average of the interpolated data The cause is not the lack of representation of the raw data by the bin averages (as illustrated in last meeting) Actual P i , Baseline P i , 3 www.windguard.de www.windguard.de

Simulation of Effect P-actual(t) P-baseline(t)=P-actaul binned lin. Interpolated P-actual binned P-baseline binned 500 450 400 350 power output [kW] 300 250 200 150 100 50 0 0 1 2 3 4 5 6 7 wind speed [m/s] PActual(t): cubic increase of P with wind speed, cp=0.45, cut-in wind speed of 3m/s, 50 (100) values per 0.5m/s (1.0m/s) wide bin, equally distributed 4 www.windguard.de www.windguard.de

Simulation of Effect for 0.5m/s wide bins P-actual binned - P-actual(t) NME: P-baseline binned - P-actual binned 14 12 10 8 deviation [%] 6 4 2 0 -2 -4 0 2 4 wind speed [m/s] 6 8 10 Simulated inner range baseline NME significant at low wind speeds 5 www.windguard.de www.windguard.de

Simulation of Effect for 1.0m/s wide bins P-actual binned - P-actual(t) NME: P-baseline binned - P-actual binned 25 20 15 deviation [%] 10 5 0 -5 0 2 4 wind speed [m/s] 6 8 10 Inner range baseline NME significantly increased compared to 0.5m/s bins 6 www.windguard.de www.windguard.de

Solution 1 to Overcome Effect (sophisticated) Treat PActualin the same way as PBaselineand PCandidate: - First bin-average PActual(t): - Then interpolate bin averages according to actual wind speed: PActual,interpolated(t) Calculate NME as: ( ) ( ) P t P t erpolated int , Actual Baseline Baseline = ( ) ( ) P t P t erpolated int , Actual Candidate Candidate = ( ) t P bin : average of P Actual i , P Actual Actual i , ( ) t ( ) t = NME Actual P , int erpolated The inner range baseline error is then zero by definition The interpolation effect cancels out in Candidateor Baseline (outer range) as PActual,interpolated(t) undergoes the same interpolation as PCandidate(t) or PBaseline(t) (outer range) 7 www.windguard.de www.windguard.de

Solution 2 to Overcome Effect (simple) Problem in case of linear interpolation between bin averages: two line assumptions with two slopes in each bin Solution: use only one line per bin, which passes through bin average, Model in bin i: i i c V m P + = 1 P P P P = + + m i 1 i i i 1 i 2 V V V V + i 1 i i i 1 = c P m V i i i i Only issue: The model reproduces the exact bin average only if the wind speed is evenly distributed over the wind speed within the bin (is mostly the case). 8 www.windguard.de www.windguard.de

Time Series Approach for Wind Resource Assessment? The interpolation problem is fully present if a bin-averaged power curve is used to simulate the power output based on a time series of the wind speed (overestimation of power at ankle of power curve, underestimation at knee) No error occurs when using a bin-averaged power curve in combination with a frequency distribution of the wind speed for the calculation of the energy production Consequence: The candidate methods may better be used only to transform the inner range power curve to the bin average of the meteorological variables (e.g. turbulence, shear) as present in the outer range. Alternative: The inner range power curve is transformed to different target values of the meteorological variables. The respective power curves in the outer range are then weighted by the frequency of each target value. 9 www.windguard.de www.windguard.de

First 4 Round Robin Tests of PCWG The former round robin tests of the PCWG are not affected by the interpolation problem: - no power measurement was used - PActual(t) has been interpolated from a binned power curve - PCandiate(t) has been calculated based on PActual(t) - As PCandiate(t) and PActual(t) are affected in the same way by the interpolation, the effect cancels out in the comparison. 10 www.windguard.de www.windguard.de

Interpolation Effect was Present also at Relative Power Curve Analysis Original Self-Consistency Test in Training Period Improved Self-Consistency Test in Training Period PC reproduced PC assumed for Training Period, rearranged deviation PC reproduced PC assumed for Training Period deviation 1.2 10 1.2 10 1.0 8 1.0 8 0.8 6 0.8 6 deviation [%] deviation [%] P/P-rated [-] P/P-rated [-] 0.6 4 0.6 4 0.4 2 0.4 2 unwanted trend 0.2 0 0.2 0 0.0 -2 0.0 -2 0.0 0.2 0.4 0.6 v/v-rated [-] 0.8 1.0 1.2 1.4 0.0 0.2 0.4 0.6 v/v-rated [-] 0.8 1.0 1.2 1.4 Approach of equal treatment of power curves helped to improve self-consistency test of Relative Power Curve Analysis 11 www.windguard.de www.windguard.de

Thank you contact: a.albers@windguard.de 12 www.windguard.de