Thermochemistry for Nonisothermal Reactor Design FA L12-1 Review

Explore the application of thermochemistry in designing nonisothermal reactors for liquid-phase exothermic reactions. Understand the energy balance, rate laws, and stoichiometry involved. Learn about terms in energy balance, steady-state conditions, and relating temperature to conversion in reactor systems. Dive into the fundamentals of heat and work interactions in reactor design.

• Thermochemistry
• Reactor Design
• Energy Balance
• Exothermic Reactions
• Rate Laws

dan_don Follow

Uploaded on Mar 05, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

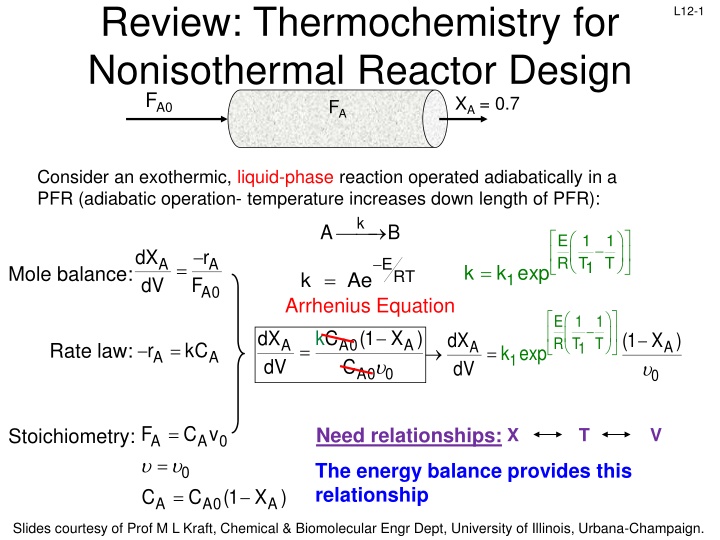
1. Review: Thermochemistry for Nonisothermal Reactor Design FA L12-1 FA0 XA = 0.7 Consider an exothermic, liquid-phase reaction operated adiabatically in a PFR (adiabatic operation- temperature increases down length of PFR): k A B E 1 R T 1 T dX dV r ERT A A = 1 = k k exp Mole balance: = k Ae 1 F A0 Arrhenius Equation E 1 1 R T 1 k C (1 X ) dX dV dX dV (1 X ) T A0 C A A = A A r kC = Rate law: = k exp A A 1 A0 0 0 = F A 0 C v = Need relationships: X T V Stoichiometry: A = The energy balance provides this relationship 0 (1 X ) C C A A0 A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

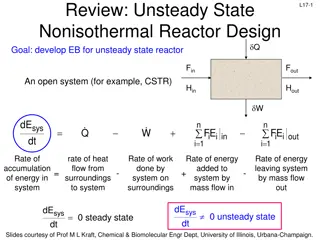
2. L12-2 Review: Terms in Energy Balance dE n n s sy ys s dt = + Q W F E F E i i i i in out = i 1 = i 1 Rate of accum of energy in system n W = Rate of work done by syst energy added to syst by mass flow in energy leaving syst by mass flow out Heat in - = - + n P : pressure iV specific volume WS: shaft work = + + FPV FPV W i i i i s in out i 1 = i 1 Flow work Internal energy is major contributor to energy term dE Q- F( dt i H E U i i n n s sy ys s = + + + W U PV ) - F( U P V ) i s i i i U n i n + i i i out = i 1 = 1 i = PV i n = + 0 Q W i0 i0 F H i i FH Steady state: s i 1 = Energy & work added by flow in i 1 = Heat in shaft work Energy & work removed by flow out Accum of energy in system - =0= - + Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

3. L12-3 Review: Relate T to Conversion n s i 1 n = + 0 Q W i0 i0 F H F H Steady state: i i = = i 1 F F ( ) i0 = + i A0 F = + i = F F X F F X where i i0 A i A0 i A i A0 dE n n s sy ys s dt ( ) = + + If XA0=0, then: Q W H i A0 F H F X s i0 i A0 i i A = i 1 = i 1 dE n n Multiply out: sys dt ( ) = + + Q W H F H F i A0 i HF X s i0 i A0 i A0 i A = i 1 = i 1 dE Total energy balance (TEB) n n s sy ys s dt ( ) = + i i i H F Q W F H H X s A0 i 0 i A0 A = i 1 = i 1 i ( ) T H heat of reaction 0 at steady state RX n n ( ) ( ) T F = + 0 Q W A0 F H H H X s i0 i i RX A0 A i 1 = i 1 = Energy & work added by flow in Energy & work removed by flow out Heat in shaft work Accum of energy in system - = - + Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

4. L12-4 Review: Q in a CSTR CSTR with a heat exchanger, perfectly mixed inside and outside of reactor FA0 = Q UA T ( T) Ta a Ta T, X T, X The heat flowto the reactor is in terms of: Overall heat-transfer coefficient, U Heat-exchange area, A Difference between the ambient temperature in the heat jacket, Ta, and rxn temperature, T Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

5. L12-5 Review: Tubular Reactors (PFR/PBR): Integrate the heat flux equation along the length of the reactor to obtain the total heat added to the reactor : A V = = Q U(T T)dA Ua(T T)dV a a a: heat-exchange area per unit volume of reactor A a V = Heat transfer to a perfectly mixed PFR in a jacket For a tubular reactor of diameter D, a = 4 / D dQ dV= Ua(T -T) a For a jacketed PBR (perfectly mixed in jacket): 1 dQ dV dQ dW Ua(T = = Heat transfer to a PBR T) a b b Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

6. L12-6 L12: Nonisothermal Reactor Design Goal: Use TEB to design nonisothermal steady-state reactors Steady state total energy balance (TEB): n s A0 i 1 Needs to be simplified before we can apply it to reactor design dE n s sy ys d t s ( ) ( ) T = = + 0 Q W F H H H F X i0 i i RX A0 A = = i 1 ( ) T TR = + At a particular temperature: H H (T ) C dT no phase change i i R pi T Ti0C dT T T T T = i 0 = + + H H H (T ) C dT H (T ) C dT pi i i 0 i R pi i R pi R R (Hi Hi0) = - (Hi Hi0) dE T n s sy ys s dt ( ) T F = Substitute Q W F i p,i C dT H X s A0 RX A0 A = i 1Ti0 T n For a SS nonisotherm flow reactor: Constant (average) heat capacities : ( ) T F = i p,i C dT 0 Q W F H X s A0 RX A0 A = i 1Ti0 n A0 i 1 = = i p,i C 0 Q W F T T H (T)F X s i0 RX A0 A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

7. Relating HRX(T) to HRX(TR) and Overall Change in Heat Capacity T n s A0 i p,i i 1Ti 0 L12-7 ( ) T = + 0 Q W F C dT H A0 F X RX A = n n ( ) T T T ( ) T T TR = + H H (T ) C dT = i i H (T ) + i pi C H d T i R X RX R P RX R R = i 1 = 1 n = i pi C overall heat capaci t y: C P = i 1 H n ( ) ( ) = overall heat of reaction at reference t emp: T i i H T RX R R = i 1 ( ) T n T TR = + + 0 Q W F i p,i C dT H ( T ) C dT F X s A0 R X R P A0 A = i 1 Ti0 Only considering constant (average) heat capacities: = i 1 T = reaction temp Ti0 = initial (feed) temp n ( ) C = + 0 Q W F i p C T T H (T ) T T F X s A0 ,i i0 R X R P R A0 A TR= reference temp Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

8. L12-8 Solving TEB for Conversion Always start with this TEB: n ( ) = + 0 Q W F i p,i C T T H (T ) C T T F X s A0 i0 RX R P R A0 A = i 1 Rearrange to isolate terms with XA on one side of eq: n ( ) + = + F i p,i C T T W Q H (T ) C T T F X A0 i0 s RX R P R A0 A = i 1 n Solve for XA: i p,i C + F T T W Q A0 i0 s i 1 = = X A ( ) + H (T ) C T T F RX R P R A0 Plug in Q for the specific type of reactor, and solve this eq simultaneously with design equation Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

9. L12-9 Solving TEB for XA for an Adiabatic Rxn s A0 i p,i i0 i 1 = Rearrange: n A0 i p,i i0 s i 1 n ( ) = + 0 Q W F C T T H (T ) C T T F X RX R P R A0 A ( ) = + F C T T Q W H (T ) C T T F X RX R P R A0 A = Which term in this equation is zero because we re solving for an adiabatic reaction? a) dEsys/dt b) c) When the reaction is adiabatic (Q=0): d) e) FA0 None of the above Q n ( ) = + F i p,i C T T Q W H (T ) C T T F X A0 i0 s RX R P R A0 A = i 1 n ( ) = + F i p,i C T T 0 W H (T ) C T T F X A0 i0 s RX R P R A0 A = i 1 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

10. L12-10 Solving TEB for XA for an Adiabatic Rxn s A0 i p,i i0 i 1 = Rearrange: n A0 i p,i i0 i 1 n ( ) = + 0 Q W F C T T H (T ) C T T F X RX R P R A0 A ( ) = + F C T T Q W H (T ) C T T F X s RX R P R A0 A = When shaft work can be neglected ( =0) and the reaction is adiabatic (Q=0): = i 1 n A0 i p,i i 1 H (T ) + i p,i i0 i 1 H (T ) C T T + T = reaction temp Ti0 = initial (feed) temperature n ( ) = + F i p,i C T T 0 0 H (T ) C T T F X A0 i0 RX R P R A0 A F C T T Solve for XA: i0 = = X A ( ) C T T F RX R P R A0 Solve this eq simultaneously with design equation Design eqs do not change, except k will be a function of T n C T T = = X A ( ) RX R P R TR= reference temp Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

11. L12-11 Nonisothermal Adiabatic Operation Constant or mean heat capacities n Q W F C ( T T )F X H ( T ) C( T T ) + = 0 s A i pi i A RX R p R 0 0 0 i = 1 Q W = = 0 0 For a system with no shaft work ( ) & adiabatic operation ( ): s n Q = 0 i pi C (T T ) i0 i 1 = = X W = 0 Xenergy balance + s H (T ) C (T T ) RX R p R CSTR, PFR, PBR, Batch C( T T ) H ( T ) Usually, Temperature p R RX R Adiabatic exothermic reactions Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

12. L12-12 Nonisothermal CSTR F X A0 r Design equation (From mass balance) : = V A Coupled Energy balance: n + = Q W F i pi C (T T ) F X H (T ) C (T T ) 0 s A0 i0 A0 RX R p R = i 1 With the exception of processes involving highly viscous materials, the work done by the stirrer can be neglected (i.e. ) = a Q UA(T With heat exchanger: A0 i pi i0 i 1 n a i pi i0 i 1 = W = 0 s T) n + = UA(T T) 0 F C (T T ) F X H (T ) C (T T ) 0 a A0 RX R p R = = + + UA(T T) F C (T T ) F X H (T ) C (T T ) A0 A0 RX R p R n UA(T T) a = + + i pi C (T T ) X H (T ) C (T T ) i0 RX R p R F = i 1 A0 n UA(T T) = a + X H (T ) C ( T T ) i pi C (T T ) RX R p R i0 F = i 1 A0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

13. L12-13 Application to CSTR Case 1: Given FA0, CA0, A, E, Cpi, H I, and XA, calculate T & V a) b) c) Solve TEB for T at the exit (Texit = Tinsidereactor) Calculate k = Ae-E/RT where T was calculated in step a Plug the k calculated in step b into the design equation to calculate VCSTR Case 2: Given FA0, CA0, A, E, Cpi, H I, and V, calculate T & XA a) b) c) Solve TEB for T as a function of XA Solve CSTR design equation for XA as a function of T (plug in k = Ae-E/RT ) Plot XA,EB vs T & XA,MB vs T on the same graph. The intersection of these 2 lines is the conditions (T and XA) that satisfies the energy & mass balance XA,EB = conversion determined from the TEB equation XA,MB = conversion determined using the design equation XA,exit Intersection is T and XA that satisfies both equations XA,MB XA XA,EB T Texit Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

14. L12-14 Application to a Steady-State PFR FA0 FA XA T distance Negligible shaft work ( S=0) and adiabatic (Q=0) a) b) c) d) Use TEB to construct a table of T as a function of XA Use k = Ae-E/RT to obtain k as a function of XA Use stoichiometry to obtain rA as a function of XA Calculate: XA A0 XA0 dX A = V F ( ) r X ,T A A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

15. A first order reaction A(l) B(l) is to be carried out adiabatically in a CSTR. Given A, E, T0, 0, CA0, and FA0, find the reactor volume that produces a conversion XA. The heat capacities of A & B are approximately equal, & S=0. a) Solve TEB for T: s A0 i p,i i0 i 1 = 0 0 L12-15 n ( ) = + 0 Q W F C T T H (T ) C T T F X RX R P R A0 A n ( ) i p,i C = + A0 F T T H (T ) C T T A0 F X i0 RX R P R A i 1 = n ( ) i p,i C = + T T H (T ) C T T X Multiply out i0 RX R P R A = i C 1 n i p,i = + C T T i p,i i0 C T H (T ) X C T X X Isolate T RX R A P A P R A = i 1 n n i p,i C + = P R C T X + + i p,i i C T C T X H (T )X T P A RX R A A 0 i 1 = i 1 = n i p,i C + = P R C T X + + T C X H (T )X p,A A0 C T Factor out T P A RX R A A i 1 = Temp when specified XA is reached Plug in values ( Cp, H RX(TR), Cp,i) given in problem statement (look them up if necessary) & solve n + P R C T + i p,i i0 C T H (T ) X X RX R A A i 1 = = T n i p,i C + C X P A = i 1 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

16. A first order reaction A(l) B(l) is to be carried out adiabatically in a CSTR. Given A, E, T0, 0, CA0, and FA0, find the reactor volume that produces a conversion XA. The heat capacities of A & B are approximately equal, & S=0. a) Solve TEB for T of reaction when the specified XA is reached: L12-16 n P R C T X + + i p,i i0 C T H (T )X RX R A A i 1 = = T n i p,i C + C X P A i 1 = b) Calculate k = Ae-E/RT where T was calculated in step (a) Look up E in a thermo book c) Plug the k calculated for the reaction s temperature when the specified XA is reached (in step b) into the design equation to calculate VCSTR A0 0 F X r F X F X 1 X C X A0 A A0 kC A A0 A A = = = = V V V V ( ) ( ) kC kC 1 X A A A0 A A0 A X 0 A = V ( ) k 1 X A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

17. L12-17 Now, the first order reaction A(l) B(l) is carried out adiabatically with and inlet temp of 300 K, CPA = 50 cal/mol K, and the heat of reaction = -20,000 cal/mol. Assume S=0. The energy balance is: A0 i p,i i0 s i A A0 R H (T ) C T T F + 0 0 n + F C T T W Q ( ) T ( ) = + H H (T ) C T T = 1 = RX RX R P R X ( ) RX R P n ( ) n i pi C T T ( ) C T T 0 i pi C 1 C = P 0 p i 1 = A = = X X A i 1 = EB EB ( ) T ( ) T H H RX RX From thermodynamics ( 20000 ) XEB 50 T 300 = X EB From energy balance T Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

18. L12-18 The irreversible, elementary liquid-phase reaction 2A B is carried out adiabatically in a flow reactor with S=0 and without a pressure drop. The feed contains equal molar amounts of A and an inert liquid (I). The feed enters the reactor at 294 K with 0 = 5 dm3/s and CA0= 1 mol/dm3. What would be the temperature inside of a steady-state CSTR that achieved XA= 0.8? Extra info: E = 10,000 cal/mol CpA= 15 cal/mol K CpB= 30 cal/mol K HA (TR) = -20 kcal/mol HB (TR) = -50 kcal/mol HI (TR) = -15 kcal/mol k = 0.02 dm3/mol s at 350 K Start with SS EB & solve for T: s 0 Q W = n A0 i p,i i 1 = A0 i p,i i0 R i 1 = i p,i i0 RX R P i 1 = n i p,i P A RX i 1 = H (T )X T C = CpI = 15 cal/mol K n i p,i C F T T H (T)F X A0 i0 RX A0 A i 1 = = 0 0 0 F C T T H (T)F X i0 RX A0 A n ) ( ) ( ) ( = + F C T T H T C T T F X X R P R A 0 A n Multiply out brackets & bring terms containing T to 1 side ( ) = + C T T H (T ) C T T X R A n + = P R C T X + + i p,i i0 C T C T C TX H (T )X R A A i 1 = n P R C T X + + i p,i i0 C T RX R A A i 1 = = n i p,i + C X P A i 1 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

19. L12-19 The irreversible, elementary liquid-phase reaction 2A B is carried out adiabatically in a flow reactor with S=0 and without a pressure drop. The feed contains equal molar amounts of A and an inert liquid (I). The feed enters the reactor at 294 K with 0 = 5 dm3/s and CA0= 1 mol/dm3. What would be the temperature inside of a steady-state CSTR that achieved XA= 0.8? Extra info: E = 10,000 cal/mol CpA= 15 cal/mol K CpB= 30 cal/mol K HA (TR) = -20 kcal/mol HB (TR) = -50 kcal/mol HI (TR) = -15 kcal/mol k = 0.02 dm3/mol s at 350 K = CpI = 15 cal/mol K n + + i p,i C H (T ) X C T X T R X R A P R A i0 i 1 = T Start with SS EB & solve for T: n i p,i C + C X P A i 1 = 1 2 cal cal bC a = C 0 = = Cp 30 15 Cp C p p p mol K mol K ( T B B A n cal cal cal o b a ( ) ( ) = = = i p,i C = 1 0 1 = 1 15 + 1 15 30m ) T R A B I mo l K ) mo ) l K l K = i 1 d a c a ( ) ( ) ( ( = + H T H T H T H H RX R D R C R R A cal mol 1 2 cal mol cal m ( ) ( ) = 5000 = 50,000 H T HR T 20,000 RX R X R o l Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

20. L12-20 The irreversible, elementary liquid-phase reaction 2A B is carried out adiabatically in a flow reactor with S=0 and without a pressure drop. The feed contains equal molar amounts of A and an inert liquid (I). The feed enters the reactor at 294 K with 0 = 5 dm3/s and CA0= 1 mol/dm3. What would be the temperature inside of a steady-state CSTR that achieved XA= 0.8? Extra info: E = 10,000 cal/mol CpA= 15 cal/mol K CpB= 30 cal/mol K HA (TR) = -20 kcal/mol HB (TR) = -50 kcal/mol HI (TR) = -15 kcal/mol k = 0.02 dm3/mol s at 350 K = CpI = 15 cal/mol K n + + i p,i C H (T ) X C T X T R X R A P R A i0 i 1 = T Start with SS EB & solve for T: n i p,i C + C X P A i 1 = n cal cal mol ( ) = C 0 i p,i C = = 30mol K H T 5000 p RX R i 1 = cal mol cal cal mol cal mol 5000 + + X 0 30mol 294 K + 5000 X 8820 A A K = = T T ca l cal + 30mol K 0 30mol K ( ) = T 427.3K = + T 166.67K 0.8 294K = X 0.8 = X 0.8 A A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

21. L12-21 The irreversible, elementary liquid-phase reaction 2A B is carried out adiabatically in a flow reactor with S=0 and without a pressure drop. The feed contains equal molar amounts of A and an inert liquid (I). The feed enters the reactor at 294 K with 0 = 5 dm3/s and CA0= 1 mol/dm3. What would be volume of the steady-state CSTR that achieves XA= 0.8? Extra info: E = 10,000 cal/mol CpA= 15 cal/mol K CpB= 30 cal/mol K HA (TR) = -20 kcal/mol HB (TR) = -50 kcal/mol HI (TR) = -15 kcal/mol k = 0.02 dm3/mol s at 350 K CpI = 15 cal/mol K F X = CSTR V A0 -r A Solve the CSTR design eq for V at XA = 0.8 & T = 427.3K: A C X ( ) = = 2 A0 2 0 A X Combine : V Ar kC = 1 X Stoichiometry :C C ( ) C STR A 2 A A0 A k C 1 A0 A 3 dm mol s 10,000cal mol 1.987cal mol K 350K 1 1 = Need at 427.3K: k k 0.02 exp 427.3 3 3 dm dm mol s ( ) = k 0.2696mol s = k 0.02 exp 2.60124 3 dm s ( ) 5 0.8 = 3 = CSTR V 370.9dm CSTR V 3 dm mol s mol dm ( ) 2 1 0.8 0.2696 1 3 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

22. L12-22 The irreversible, elementary liquid-phase reaction 2A B is carried out adiabatically in a flow reactor with S=0 and without a pressure drop. The feed contains equal molar amounts of A and an inert liquid (I). The feed enters the reactor at 294 K with 0 = 5 dm3/s and CA0= 1 mol/dm3. Use the 2-point rule to numerically calculate the PFR volume required to achieve XA=0.8? Extra info: E = 10,000 cal/mol CpA= 15 cal/mol K CpB= 30 cal/mol K HA (TR) = -20 kcal/mol HB (TR) = -50 kcal/mol HI (TR) = -15 kcal/mol k = 0.02 dm3/mol s at 350 K Use the energy balance to construct table of T as a function of XA For each XA , calculate k, -rA and FA0/-rA Use numeric evaluation to calculate VPFR XA T(K) k(dm3/mol s) 0 294* 0.8 427.3* 0.2696* *Calculated in CSTR portion of this problem 3 dm 1 k 0.02 exp 5032.7126K mol s 350K dm r 0.00129 mol s 3 dm mol r 0.2696 1 1 0.8 mol s dm CpI = 15 cal/mol K -rA(mol/dm3 s) 0.00129 0.010784 FA0/-rA(dm3) 0.00129 3 1 dm = = k 0.00129mol s 294 3 2 mol dm mol dm s ( ) ( ) 2 2 = 1 0 = = 1 X 2 1 r 0.00129 r kC A A A A0 A 6 3 = = X 0 X 0 A A 2 mol dm s ( ) 2 = = r 0.010784 A A 6 3 = = X 0.8 X 0.8 A A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

23. L12-23 The irreversible, elementary liquid-phase reaction 2A B is carried out adiabatically in a flow reactor with S=0 and without a pressure drop. The feed contains equal molar amounts of A and an inert liquid (I). The feed enters the reactor at 294 K with 0 = 5 dm3/s and CA0= 1 mol/dm3. Use the 2-point rule to numerically calculate the PFR volume required to achieve XA=0.8? Extra info: E = 10,000 cal/mol CpA= 15 cal/mol K CpB= 30 cal/mol K HA (TR) = -20 kcal/mol HB (TR) = -50 kcal/mol HI (TR) = -15 kcal/mol k = 0.02 dm3/mol s at 350 K Use the energy balance to construct table of T as a function of XA For each XA , calculate k, -rA and FA0/-rA Use numeric evaluation to calculate VPFR XA T(K) k(dm3/mol s) 0 294 0.00129 0.8 427.3 0.2696 CpI = 15 cal/mol K -rA(mol/dm3 s) 0.00129 0.010784 FA0/-rA(dm3) 3876 463.6 3 mol dm dm s mol s = = F 1 5 5 = F C A0 3 A0 A0 0 mol s mol s 5 5 F F = = = = 3 3 3876 dm 463.6 dm A0 r A0 r mol mol 0.00129dm s 0.010784dm s A A = = X 0 X 0.8 A A 3 3 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.

24. L12-24 The irreversible, elementary liquid-phase reaction 2A B is carried out adiabatically in a flow reactor with S=0 and without a pressure drop. The feed contains equal molar amounts of A and an inert liquid (I). The feed enters the reactor at 294 K with 0 = 5 dm3/s and CA0= 1 mol/dm3. Use the 2-point rule to numerically calculate the PFR volume required to achieve XA=0.8? Extra info: E = 10,000 cal/mol CpA= 15 cal/mol K CpB= 30 cal/mol K HA (TR) = -20 kcal/mol HB (TR) = -50 kcal/mol HI (TR) = -15 kcal/mol k = 0.02 dm3/mol s at 350 K Use the energy balance to construct table of T as a function of XA For each XA , calculate k, -rA and FA0/-rA Use numeric evaluation to calculate VPFR XA T(K) k(dm3/mol s) 0 294 0.00129 0.8 427.3 0.2696 CpI = 15 cal/mol K -rA(mol/dm3 s) 0.00129 0.010784 FA0/-rA(dm3) 3876 463.6 X 1 h ( ) ( ) ( ) 2-point rule: f x dx f X f X where h X X h 0 8 . h 0 8 . = + = = = 0 0 1 1 0 2 X 0 . 0 83876 2 3 3 V dm . dm = + 463 6 PFR 3 V dm = 1736 PFR Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.