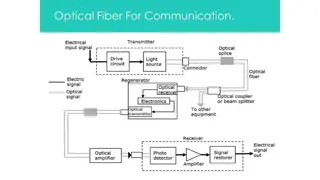
Time and Amplitude Scaling in Signals
Time and Amplitude Scaling are fundamental concepts in signal processing. Time scaling involves adjusting the speed and period of a signal, while amplitude scaling focuses on changing the amplitude without altering the shape. The mathematical representations and examples provided in the content illustrate the impact of these scaling operations on signals. Understanding these principles is crucial for signal analysis and manipulation.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Time Scaling Time scaling refers to the multiplication of the time variable of a time signal x(t) by a real positive constant a . Mathematically, we can write y(t) = x(at) For the given function x(t), x(at) is the time scaled version of x(t) For a 1,period of function x(t) reduces and function speeds up. The graph of the function gets compressed. For a 1, the period of the x(t) increases, and the function slows down. The graph of the function expands.
Example: For given x(t), find y(t) = x(2t). The period of x(t) is 2 and the period of y(t) is 1.
Given x(t), Find y(t) = x(3t) and v(t) = x(t/3).
Amplitude Scaling Amplitude scaling refers to the multiplication of the time signal x(t) by a real positive constant A . Mathematically, it can be represented as y(t) = Ax(t) The amplitude of y(t) at any instant is equal to A times the amplitude of x(t) at that instant, but the shape of y(t) is same as the shape of x(t). For the given function x(t), Ax(t) is the amplitude scaled version of x(t). For A 1, it is amplification. For A 1, it is attenuation.
Examples of Amplitude Scaling Plots of (a) Signal x(t) (b) y(t)=2x(t)
References 1. Signals and Systems - A. Anand Kumar, PHI Publications, 2nd edition, 2012. 2. Fundamentals of Signals and Systems - Benoit Boulet, Charles River Media, 2006.