Tree Diagrams and Mutually Exclusive Events in Probability
Explore the concept of tree diagrams and mutually exclusive events in probability through a series of examples and questions. Learn how to analyze different outcomes, calculate probabilities, and make informed decisions based on the given scenarios.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
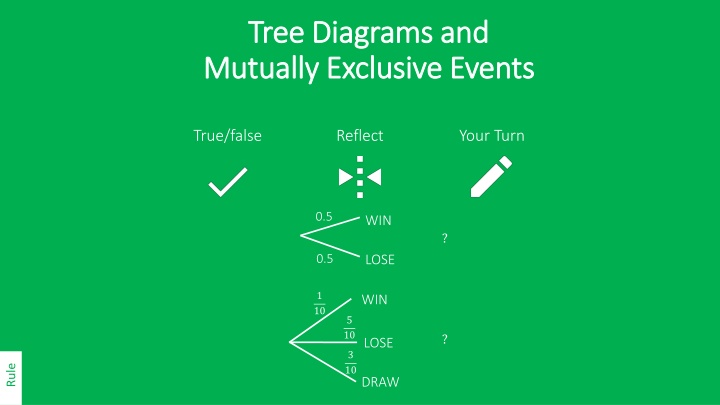
Tree Diagrams and Tree Diagrams and Mutually Exclusive Events Mutually Exclusive Events True/false Reflect Your Turn 0.5 WIN ? 0.5 LOSE 1 10 WIN 5 10 ? LOSE 3 10 Rule DRAW
3 2 4 WIN 10 5) 1) 0.5 WIN WIN Y / N Y / N 9) Y / N LOSE 7 LOSE LOSE 2 8 0.5 10 1 2 10) 6) 0.25 WIN WIN 0.3 WIN Y / N Y / N 2) Y / N 2 2 LOSE 0.25 LOSE LOSE 0.3 1 2 11) 0.3 WIN 7) WIN 0.3 3) WIN Y / N Y / N Y / N LOSE 1 2 LOSE -0.7 LOSE 0.7 1 8) 12) 1 WIN WIN Y / N 0.5 Y / N 4) WIN Y / N LOSE 0.5 LOSE 0 LOSE 1 Graeme.Mitchinson@excelsiornewcastle.org.uk
3 2 4 WIN 10 5) 1) 0.5 WIN WIN Y / N Y / N 9) Y / N LOSE 7 LOSE LOSE 2 8 0.5 10 1 2 10) 6) 0.25 WIN WIN 0.3 WIN Y / N Y / N 2) Y / N 2 2 LOSE 0.25 LOSE LOSE 0.3 1 2 11) 0.3 WIN 7) WIN 0.3 3) WIN Y / N Y / N Y / N LOSE 1 2 LOSE -0.7 LOSE 0.7 1 8) 12) 1 WIN WIN Y / N 0.5 Y / N 4) WIN Y / N LOSE 0.5 LOSE 0 LOSE 1 Graeme.Mitchinson@excelsiornewcastle.org.uk
TEA 0.10 Y / N Y / N WIN 2 8 5 8 13) 0.20 COKE LOSE 15) 1 8 0.20 JUICE DRAW 0.50 COFFEE 1 4 TEA 1 4 16) WIN 0.25 Y / N COKE 14) 0.50 1 4 Y / N LOSE 0.75 JUICE 1 4 DRAW COFFEE Graeme.Mitchinson@excelsiornewcastle.org.uk
TEA 0.10 Y / N Y / N WIN 2 8 5 8 13) 0.20 COKE LOSE 15) 1 8 0.20 JUICE DRAW 0.50 COFFEE 1 4 TEA 1 4 16) WIN 0.25 Y / N COKE 14) Y / N 0.50 1 4 LOSE 0.75 JUICE 1 4 DRAW COFFEE Graeme.Mitchinson@excelsiornewcastle.org.uk
Your Turn WIN 1 10 WIN 0.4 1) 5 10 Y / N 3) Y / N 0.5 LOSE LOSE 4 10 0.1 DRAW DRAW 1 3 TEA Y / N 1 2 WIN Y / N 1 3 1 2 1 2 2) 4) COKE LOSE 1 3 JUICE DRAW 1 3 COFFEE Graeme.Mitchinson@excelsiornewcastle.org.uk
Your Turn - Answers WIN 1 10 WIN 0.4 1) 5 10 Y / N 3) Y / N 0.5 LOSE LOSE 4 10 0.1 DRAW DRAW 1 3 TEA Y / N 1 2 WIN Y / N 1 3 1 2 1 2 2) 4) COKE LOSE 1 3 JUICE DRAW 1 3 COFFEE Graeme.Mitchinson@excelsiornewcastle.org.uk