Triangle Angle Theorems
Explore the Triangle Sum Theorem and Exterior Angle Theorem to solve for missing angles in triangles. Practice classifying triangles and understand how interior and exterior angles are related in geometric shapes.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
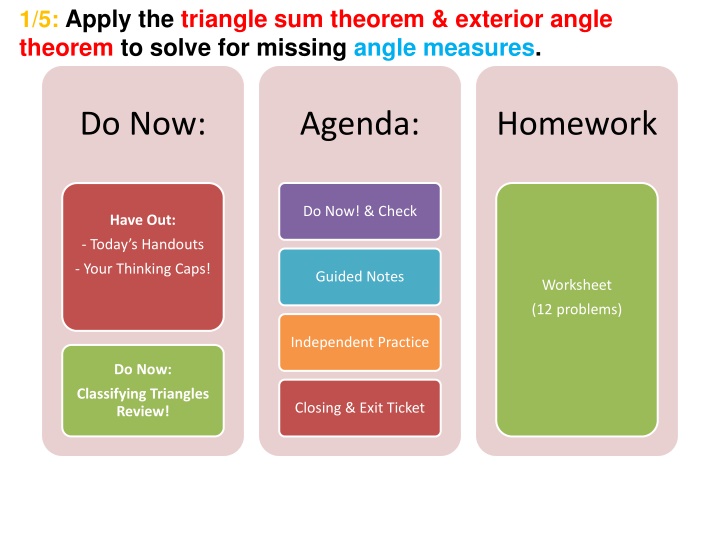
1/5: Apply the triangle sum theorem & exterior angle theorem to solve for missing angle measures. Do Now: Agenda: Homework Do Now! & Check Have Out: - Today s Handouts - Your Thinking Caps! Guided Notes Worksheet (12 problems) Independent Practice Do Now: Classifying Triangles Review! Closing & Exit Ticket
Apply the triangle sum theorem & exterior angle theorem to solve for missing angle measures. When you finish Do Now: Flip Over Write down objective Complete warm-up
E 87 145 180 - 145 m DFE = 35 58 35 58 + 35 + DEF = 180 m DEF = 87 145 145 When you add the two non-adjacent interior angles together, you get the measure of the exterior angle.
The sum of the three interior angle measures of any triangle is equal to 180 In + In + In = 180 The sum of the two nonadjacent interior angle measures of any triangle is equal to the measure of the exterior angle. In + In = Out
Triangle Exterior Angle Theorem In + In = Out 30 + 42 = m 2 72 108 m 2 = 72 Obtuse Triangle
Triangle Exterior Angle Theorem In + In = Out 75 145 35 x + 70 = 2x 5 + 5 + 5 x + 75 = 2x -x -x 75 = x m JKM = 2x 5 m JKM = 2(75) 5 m JKM = 145 Acute Triangle