Triangle Ratios and Similarity
Trigonometry concepts such as ratios of sides in right-angled triangles are explored through the angles, hypotenuse, and opposite/adjacent sides. Discover the relationships between angles, sine, cosine, and similarity in triangles through practical examples. See how these key elements connect to determine missing lengths and angles in geometric calculations.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
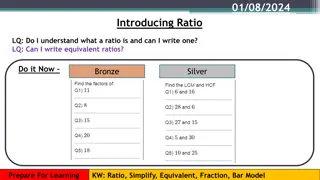
Discuss: What do these triangles have in common? Try to include these key words in your discussion: Angle Similar Ratio Hypotenuse Opposite
The ratio of the opposite side to the hypotenuse in any right-angled triangle is called the SINE ratio. The ratio of the opposite side to the hypotenuse in any-right angled triangle for any angle can be found using a table or your calculator.
60 60 60 Discuss: What do these triangles have in common? Try to include these key words in your discussion: Angle Similar Ratio Hypotenuse Adjacent
The ratio of the adjacent side to the hypotenuse in any right-angled triangle is called the COSINE ratio. COSINE = SINE of the COMPLEMENT
The ratio of the opposite side to the hypotenuse in any right-angled triangle is called the SINE ratio. ???????? ????????? sin? = The ratio of the adjacent side to the hypotenuse in any right- angled triangle is called the COSINE ratio. ???????? ????????? cos? =
On your whiteboards: What is the value of ????? ???????? ????????? ???????? ????????? cos? = sin? =
On your whiteboards: What is the value of ????? ???????? ????????? ???????? ????????? cos? = sin? =
On your whiteboards: What is the value of ?????
Teddy and Dora are calculating the missing length ?. Dora You should use cosine. ? 32 Jack 20 cm You should use sine. Who s right, Jack or Dora? Can they both be right? Explain your answer. Show that the missing value ? is 17.0 cm.
Title: Using the Sine and Cosine ratios to find missing lengths. The ratio of the opposite side to the hypotenuse in any right-angled triangle is called the SINE ratio. ???????? ????????? sin? = The ratio of the adjacent side to the hypotenuse in any right- angled triangle is called the COSINE ratio. ???????? ????????? cos? =
Worked Example Your Turn 8 ?? 45 3 ?? ? ? 33 sin 45 =8 ? ? ??? 45 = 8 8 ? = sin45 ? = 11.3 cm 3 significant figures
Some people find calculation triangles, like those used in Science, useful to know whether to multiply or divide ???????? ????????? sin? = Finding the opposite Finding the hypotenuse
Further consolidation 1 Copy the questions and calculate the missing lengths to 3 significant figures using Sine. ? ? ?) ???? BC ?
Mark your work a) 7.55 b) 6.66 c) 28.6 d) 30.1
Some people find calculation triangles, like those used in Science, useful to know whether to multiply or divide ???????? ????????? cos = Finding the adjacent Finding the hypotenuse
Further consolidation 2 Copy the questions and calculate the missing lengths to 2 decimal places using Cosine ? ? ? ?
Mark your work: Copy the questions and calculate the missing lengths to 2 decimal places. a. 2.08 b. 15.6 c. 18.4 d. 7.97 ? ? ? ?