Triangles Review: Solving Angles, Area, Solutions, Elevation
This content covers various problems related to solving triangles, angles, area, and practical applications such as angle of elevation. It includes finding angles and area in isosceles triangles, determining solutions in triangles, calculating distance in real-life scenarios, and exploring properties of parallelograms. The examples provided offer a practical understanding of triangle concepts and applications.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
CHAPTER 9 REVIEW Solving Triangles
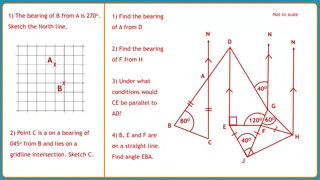
FIND THE ANGLES AND AREA In isosceles triangle with sides 10, 10, and 15ft, find all the angles to the nearest degree and the area to the nearest unit. Angles: 41o, 41o, 98o Area: 49ft2
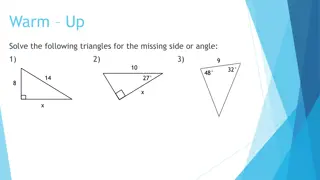
HOW MANY SOLUTIONS? In a triangle b = 5, c = 10, B = 20o 2 Solutions
ANGLE OF ELEVATION An airplane flies at an altitude of 10,000ft. The angle of depression from the plane to a tree is 13o. How far must the plane fly to be directly over the tree? Round to the nearest foot. 43,315ft
ANGLE OF ELEVATION Bill determines the angle of elevation to the top of a building measures 40o. If he walks 102 feet closer to the building the angle of elevation is 55o. Find the height of the building to the nearest foot. 208ft
A parallelogram has side lengths 16 and 20in. One angle of the parallelogram measures 120o. Find each diagonal to the nearest tenth. 31.2in and 18.3in
AREA The vertex angle of an isosceles triangle is 150o. If the area is 9cm2, find each leg. Each leg = 6cm
FIND THE AREA TO THE NEAREST UNIT. 417u2
NAVIGATION An airplane flies on a course of 130o at a speed of 1100km/h. How far east of its starting point is it after 3 hours? Round to the nearest km. 2528km
NAVIGATION A ship leaves port and proceeds west 30 miles. It then changes course to 20o until it is due north of its origin. How far north of its origin is it? Round to the nearest mile. 82miles
SURVEYING From the mall proceed 500m northeast to the Target, then 300m east along the highway to the gas station, then 200m S15oE to the edge of Woodbourne Road and finally along Woodbourne Road back to the mall. 125,000m2
SURVEYING From the southeast corner of the cemetery on Burnham Road, proceed S78oW for 250m along the southern boundary of the cemetery until a granite post is reached, then S15oE for 180m to Allard Road, then N78oE 300m along Allard Road until it intersects Burnham Road, and finally N30oW along Burnham Road back to the starting point. Sketch the plot and find the area. 49,500 ft2