Trigonometry: Calculator Functions and Taylor Polynomials
The inner workings of calculators in determining trigonometric values like sin, cos, and tan, as well as the process of finding Taylor polynomials to approximate functions. Dive into the details of these mathematical concepts and enhance your understanding.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
mastermathmentor.com presents CALCULUS ON THE WALL 20. Taylor PolynomialsHelping students learn and teachers teach Created by: Stu Schwartz Sample Version Unnarrated Graphics: Apple Grapher: Version 2.3 Math Type: Version 6.7 Intaglio: 2.9.5a Fathom: Version 2.11
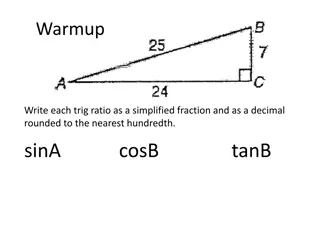
The Basics On your calculator, change to degree mode and find sin 56 , cos 56 , and tan 56 . Can you explain what the calculator is finding and how it finds it? If we have a unit circle (radius = 1) and draw a 56 angle, sin 56 is the ratio of y to 1 which is y. So, in this unit circle, the height of this triangle is 0.8290375726. Similarly, cos 56 is x, the base of the triangle and has the value of 0.5591929035. And tan 56 is the ratio of y to x which is 1.482560969. How does the calculator determine these values? One possibility is that it has values memorized. But assuming that the calculator can find trig functions of angles from 10 million to 10 million degrees using thousandths of degrees, the table below, accurate to 10 decimal places, would use 1.9 gigabytes of memory. So if the calculator hasn t memorized these values, it must be doing something else when taking trig functions. It may surprise you that the only capabilities of even the most advanced calculator are addition, subtraction, multiplication, and division. Angle 55.8 55.9 56.0 56.1 56.2 sine cosine tangent 0.827080574 0.562083378 1.471455316 0.828060335 0.560638995 1.476993828 0.829037573 0.559192903 1.482560969 0.830012285 0.557745109 1.488156995 0.830984469 0.556295616 1.493782166 www.mastermathmentor.com
More Accuracy We will gain more accuracy by using increasing the degree of our approximating polynomial. For each polynomial, the function f(x) = exand the polynomial will have the same value at x = 0 as well as every derivative. We will use the polynomials to approximate e0.1 whose real value is 1.105170918. Degree 2 P2(x) = a0 + a1x +a2x2 Degree 3 P3(x) = a0 + a1x +a2x2 + a3x3 Degree 4 P4(x) = a0 + a1x +a2x2 + a3x3 + a4x4 P 0 ( ) = f 0 ( ) P 0 ( ) = f 0 ( ) P P 0 ( ) = f 0 ( ) P 0 ( ) = f 0 ( ) P P 0 ( ) = f 0 ( ) P 0 ( ) = f 0 ( ) P a0=1 a1=1 2a2=1 a2=1 a0=1 a1=1 2a2=1 a2=1 a0=1 a1=1 2a2=1 a2=1 0 ( ) = f 0 ( ) 0 ( ) = f 0 ( ) 0 ( ) = f 0 ( ) 2 2 2 0 ( ) = 0 ( ) 6a3=1 a3=1 P f 6a3=1 a3=1 0 ( ) = 0 ( ) P2x ( ) =1+ x+x2 P20.1 ( ) =1.105 P f 6 6 2 4 ( )0 ( )= f 4 ( )0 ( ) P3x ( ) =1+ x+x2 2+x3 24a4=1 a4=1 P P30.1 ( ) =1.105166667 24 6 P4x ( ) =1+ x+x2 2+x3 6+x4 P40.1 ( ) =1.105170833 24 www.mastermathmentor.com
Finding a Taylor Poynomial The best way to find Taylor polynomials is to create a chart with two columns. The first column contains the function and its subsequent derivatives and the second column evaluates the first column at c. Find the Taylor polynomials, P1, P2, P3, P4 and P5 for f(x) = ln x centered at c = 1 And use each to approximate ln 1.1 (which is 0.0953102). f x ( ) = lnx x ( ) = x-1=1 f 1 ( )= 0 f 1 ( ) =1 1=1 f x 1 ( ) =-1 x ( ) = -x-2=1 12= -1 f f x2 x ( ) = 2x-3=2 1 ( ) =2 13= 2 f f x3 4 ( )1 ( ) =-6 4 ( )x ( ) = -6x-4=6 14= -6 f f x4 P1x ( ) = 0+1 x-1 ( ) = x-1 P11.1 )-1 x-1 2! )-1 x-1 2! )-1 x-1 2! ( ) = 0.1 ( Without going through the analysis, the pattern suggests that the 5th degree ( ( ) ) 2 2 x-1 2 P2x ( ) =1 x-1 ( = x-1 ( )- ( ) = 0.95 P21.1 ) 5 ( ) ( ) ( ) ( ) term in P5x ( ) is +x-1 2 3 2 3 +2 x-1 x-1 2 x-1 3 x-1 ( P3x ( ) =1 x-1 ( = x-1 ( )- ( ) = 0.95333 + . It is. P31.1 3! 5 ( ) ( ) ( ) ) ( ) ( ) 2 3 4 2 3 4 +2 x-1 -6 x-1 x-1 3 x-1 4 P4x ( ) =1 x-1 ( = x-1 ( )- ( )= 0.95308 + - P41.1 3! 4! 2 www.mastermathmentor.com
Explaining Lagrange We explain the Lagrange Error by analogy. Ted wants to know exactly how far it is to Lisa s house. He gets explicit directions from his house to hers and has to make the turns as shown in the figure. He travels the 20 miles and gets to the loop. He realizes then that he has lost her address. He knows she lives at some house on the mile-long loop but doesn t know exactly which house is hers. So when he reaches the loop, he is a maximum of mile from her house. He may be closer but the maximum distance that he would still have to travel if he knew her address would be mile. That is what the Lagrange error finds. The nth degree Taylor polynomial approximates the value of f(x) at some value a. The Lagrange error gives the maximum amount that this approximation deviates from the true value of f(a). The actual error may in fact be smaller, just as when Ted reaches the loop, he may be less than mile from Lisa s house. But the Lagrange error gives an outer bound of the error. It represents a worst-case scenario. www.mastermathmentor.com
Purchase the full version - 15 slides Content: Taylor Polynomials www.mastermathmentor.com Powerpoint slides to help teach in the classroom Only $10.95 for the full presentation of 15 content slides. (download version) You receive: A narrated version (83 megs) An un-narrated version (2 megs) A PDF of the narration used if you want to provide the commentary Note: Downloading the full presentation may require high-speed internet. Or purchase the entire set of MasterMathMentor.com BC Calculus On the Wall Powerpoint presentations - Only $69.95 - sent to you on a 2-gig flash drive. Topics cover: L Hospital s Rule Integration Techniques Euler s Method & Logistic Growth Parametric and Polar Equations Vector-Valued Functions Taylor Polynomials Infinite Series Power Series www.mastermathmentor.com