Trigonometry: Real Life Applications and Fundamentals

CLASS-X MATHEMATICS TOPIC:APPLICATIONS OF TRIGONOMETRY

PDF OF THE CHAPTER PDF OF THE CHAPTER http://www.ncert.nic.in/ncerts/l/jemh109.pdf

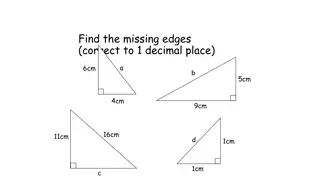
LEARNING OBJECTIVES: LEARNING OBJECTIVES: Students will be able to: Define the six trigonometric ratio for a given angle. Apply the definitions of angle of elevation and angle of depression in real life applications. Apply the six trigonometric ratios of an acute angle in a right triangle. Find the reference angle for a given triangle. Apply the properties of reference angles in appropriate situations. Understand the trigonometric complimentary angle relations. Predict what would happen when the value of adjacent , opposite , and hypotenuse is changed. To determine the height or the depth of an object at a certain distance using trigonometric ratios. For example: We can calculate the height of a tower by standing a certain distance away from it and calculating the angle of elevation, thereby determining the height of the tower.

CONTENTS: CONTENTS: CONCEPT-3 INTRODUCTION CONCEPT BASED QUESTION PREVIOUS KNOWLEDGE QUESTIONS CONCEPT-4 REAL LIFE APPLICATIONS CONCEPT BASED QUESTION THE TRIGONOMETRIC TABLE CONCEPT-5 BASIC FUNDAMENTALS CONCEPT BASED QUESTION INTERESTING FACT CBSE BOARD QUESTION 2020 EXAMPLES HOTS QUESTION FOR YOU CONCEPT-1 ACTIVITY CONCEPT BASED QUESTION MIND MAP CONCEPT-2 INTERESTING FACT CONCEPT BASED QUESTION SUMMARY

INTRODUCTION INTRODUCTION Trigonometry is a Greek-originated word where Tri means three, gon means sides and Metry means measure. It is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century B.C. from applications of geometry to astronomical studies.

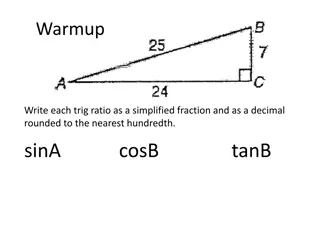
PREVIOUS KNOWLEDGE QUESTIONS: 1. In a ABC, right angled at B, tan A= 24 7 , find the other trigonometric ratios of angle A 2. In the ABC , right angled at B , if A = C = 45 , then prove that (i) sin A = sin C (ii) cos A = cos C (iii) sin A + cos A = 2 (iv) tan A + cot A = 2 3. In a right angle ABC right angled at B what does tan C represent? 4. If ABC is right angled at C, then find the value of cos(A+B). 5. If sin A = 1 2 , then the value of cot A is ________. 6. What is the value of tan(90 - )?

REAL LIFE APPLICATIONS: REAL LIFE APPLICATIONS: Trigonometry is used in various fields. It has applications in wider fields like engineering, physics, surveyors, architects, astronauts and even investigation of a crime scene. Apart from astronomy and geography, trigonometry is applicable in various fields like satellite navigation, developing computer music, chemistry number theory, medical imaging, electronics, electrical engineering, civil engineering, architecture, mechanical engineering, oceanography, seismology, phonetics, image compression and game development.

TRIGONOMETRY IN REAL LIFE TRIGONOMETRY IN REAL LIFE

THE TRIGONOMETRIC TABLE THE TRIGONOMETRIC TABLE

BASIC FUNDAMENTALS BASIC FUNDAMENTALS ANGLE OF ELEVATION: The angle of elevation of an object as seen by an observer is the angle between the horizontal and the line from the object to the observer s eye (the line of sight).

BASIC FUNDAMENTALS BASIC FUNDAMENTALS ANGLE OF DEPRESSION: If the object is below the level of the observer, then the angle between the horizontal and the observer s line of sight is called the angle of depression.

Example 1: A ladder is leaning against a wall to a height of 5 m. If the length of the ladder is 10 m, Find-: the angle between the ladder and the horizontal ground. At what distance from the wall the base of the ladder is? Ans: Here denotes the angle of elevation. We can measure it by taking A sine of the angle ????????????? ????????? =?? sin = ?? 10 m sin = 1 5 m 2 sin = sin30 = 30 ? C B

Now we need to find the distance which the foot of the ladder is from the wall i.e. the length of BC We know tan = ???? = tan = ?? 1 ?? BC=5 3 ?. ????????????? ?? ?? ?? tan 30 = 5 ? 3=5 ? ??

Example 2: Find the Suns elevation if a pole 6m high casts a shadow 2 3 m long on the ground. Solution: In given triangle, let BC = 6m be the height of the pole. C AB = 2 3 be the length of the shadow on the ground. Let the Sun s makes an angle ? on the ground. Now, in BAC, tan = ?? ?? 6 2 3 = 3 tan = 3 3 3 = 3 = tan60 =60 Hence, the Sun s elevation is 60 . 6 m 3 3 = 3 3 tan = 3 ? 3 B A 2 3 m MARKING SCHEME FOR CORRECT FIGURE- 0.5 FOR FINDING RATIO- O.5 FOR CORRECT VALUE OF - 1

TYPE-1: When the observer is a point object Question 1: A tower stands vertically on the ground from a point on the ground which is 15 m away from the foot of the tower. The angle of elevation of the top of the tower is 60 . Find the height of the tower A Solution: In the given figure, we need to find AB where BC is given. So, using formula: tan = ?? ?? 60 tan 60 = ?? C B ?? 15 m 3 =?? 15 AB = 15 3 m

CONCEPT BASED QUESTION 1. A tower is 50m high. Its shadow is ? m shorter when the Sun s altitude is 45 than when it is 30 . Find ? correct to the nearest cm. 2. A ladder is placed against a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 8m away from the foot of the wall and the ladder is making an angle of 30 with the level of the ground. Determine the height of the wall. (Take 3 = 1.732)

TYPE-2: When height of the object is given Question 2: An observer of 1.5m tall is 28.5m away from a chimney. The angle of elevation of the top of the chimney from the observer s eyes is 45 . What is the height of the chimney? A 45 C Ans: In the given figure ED = BC = 28.5m BE = CD = 1.5m ABC = 45 (In every plane the angle of elevation is made with the horizontal line at that point.) B 1.5 m 1.5 m 28.5 m E D

In ABC, ????????????? ???? ?? ?? tan = = tan45 =?? ?? 1 = ?? 28.5 Height of the chimney = AD = CD+AC So, AC = 28.5m. = (1.5+28.5)m = 30m.

CONCEPT BASED QUESTION 1. From the top of a cliff 50m high, the angles of depression of the top and bottom of a tower are observed to be 30 and 45 , respectively. Find the height of the tower. 2. From a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30 . The angle of elevation of the top of a water tank (on the top of the tower) is 45 . Find the (i) height of the tower (ii) the depth of the tank.

TYPE-3: When the angle of depression is given Question 3: The angle of depression from the top of a 20 m tall building to a man on the ground is 60 . Find the distance of the man from the foot of the building. Solution: In the right ABC, S A AB=20 m BCA= CAS=60 ?? ????????= ??? ? So, Cot 60 =?? ?? 1 20 BC=20 3 Hence, distance of man from the foot of the building is 20 3 60 ??=???????? 20 m 3=?? 60 B C 3 = 20 3 3 m.

CONCEPT BASED QUESTION 1. As observed from the top of a light house, 100m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30 to 45 .Determine the distance travelled by the ship during the period of observation. 2. A straight highway leads to the foot of a tower . A man standing at the top of the tower observes a car at an angle of depression of 30 , which is approaching the foot of the tower with a uniform speed . Six minutes later, the angle of depression of the car is found to be 60 .Find the further time taken by the car to reach the foot of the tower.

TYPE-4: When there are more than one angle of elevation from the same point. Question 4: A statue 1.6m tall stands on the top of a pedestal. From the same point the angle of elevation of the top of the statue is 60 . From the same point the pedestal is 45 . Find the height of the pedestal. A Solution: In the right ACD, 1.6 m AB = 1.6m, BDC = 45 , ADC = 60 In the triangles ACD and BCD, CD is common. So, in right ACD, tan60 =?? B 60 ?? 45 ??+1.6 ?? 3 = D C CD=??+1.6 (i) 3

In right BCD , tan45 =?? ?? 1 = ?? ?? So BC = CD (ii) Putting the value of BC from EQ-(ii) in EQ(i) We get, CD=??+1.6 3 3 CD=CD+1.6= 3 CD CD = 1.6 ( 3-1) CD = 1.6 1.6 3 1 CD = 3+1 3+1=1.6( 3+1) 1.6 3 1 = 2.18 Therefore BC = CD = 2 = 2.18 m

CONCEPT BASED QUESTION 1. A 1.2m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60 . After some time, the angle of elevation reduces to 30 .Find the distance travelled by the balloon during the interval. 2. The angle of elevation of the top of an unfinished tower at a point distant 100 m from its base is 45 ; how much higher must the tower be raised so that its angle of elevation at the same point may be 60 ? (Take 3 = 1.73)

TYPE-5: Where both angle of elevation and angle of depression are given Question 5: From the top of a 10 m building the angle of elevation to the top of another building on the same plane is 30 whereas the angle of depression to the bottom is 60 . Find the height of the other building. Solution: AB=CD=10 m E EAD=30 , DAC=60 , ACB=60 . In ABC, Cot 60 =?? 30 A ?? D 3=?? AD=10 1 10 BC=10 60 3 10 m 3 ..(i) In right EAD, Tan 30 =?? 60 ?? C B 1 3=?? 1 3 10 3=10 ED= 3 (ii) 10 3 Height of another building EC=ED+CD =10+10 3 =40 3 m= 131 3 m

CONCEPT BASED QUESTION 1. From the top of a 7m high building, the angle of elevation of the top of a cable tower is 60 and the angle of depression of its foot is 45 .Determine the height of the tower. 3. A window of a house is h m above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be ? and ?, respectively. Prove that the height of the other house is h(1 + tan? cot ? )m

CBSE BOARD QUESTION 2020 From the top of a 7 m building, the angle of elevation of the top of a cable tower is 60 and the depression of its foot is 45 . Determine the height of the tower. (Use 3 = 1.73)27 In ABC, tan 45 =?? ?? 1= 7 ? ?? BC=7 m. Also, AD=BC=7 m In ADE, tan 60 = ?? ?? 3 = 7 ? DE=7 3m E 60 A D 45 7 m 7 m ?? 45 C B Total height of the tower:(7+7 3)m=7(1+ 3)m FOR CORRECT FIGURE- 1 FOR FINDING THE VALUE OF BASE- 11 FOR FINDING THE LENGTH OF DE- 1 FOR FINDING THE TOTAL HEIGHT-1 2 2

HOTS HOTS The angle of elevation of the top of a tower from two points at a distance a m and b m from the base and in the same straight line are complimentary. Prove that height of the tower is ?? m. Sol: CD=h, BC=a, AC=b DBC= , DAC=(90 ) In right DCB, tan =?? ? ? In right DCA, tan (90 )=?? ? (??) Multiplying each side of ???? & ?? , we get- tan cot = ? 1= 2 D ??= ??= h ? 90 -? ? A B C a ??= 2=ab h= ?? m b

QUESTION FOR YOU QUESTION FOR YOU The angles of depression of the top and bottom of an 8 m tall building from top of a multistoried building are 30 and 45 respectively. Find the height of the multistoried building and the distance between the two buildings.

ACTIVITY ACTIVITY OBJECTIVE: OBJECTIVE: To find out the height of a pole. PRE PRE- - REQUISITE KNOWLEDGE: REQUISITE KNOWLEDGE: (i) TRIGONOMETRIC RATIOS (ii) TRIGONOMETRIC TABLE MATERIALS REQUIRED: MATERIALS REQUIRED: (i) COMPLETE PROTRACTOR (ii) A THIN PIPE OF ALUMINIUM (iii) A PROTRACTOR FIXED ON A STAND (iv) MEASURING TAPE

Continued PROCEDURE: PROCEDURE: (i) Fix a pipe of aluminium at centre of protractor in such a way that the pipe is free to rotate (ii) Rotate the pipe in such a way that the top of the pole is visible through the pipe (iii) Observe the angle of elevation of the top of the pole and note it, say ? = 45 (iv) Measure the horizontal distance between the pole and the point of observation, say ?=10 m (v) Measure the height of point of the observation from the ground say =1m

Continued OBSERVATION: OBSERVATION: 1. Angle of elevation = ? = 45 2. Distance between point of observation and pole d=10m 3. Height of the point of observation from the ground = 1m CALCULATION: CALCULATION: Let the height of the pole be ? tan ?=? tan45 =? 1 ? 10 1=? 1 10 ? 1 = 10 ? =11 m

Continued CONCLUSION: CONCLUSION: The height of the pole is 11 m LEARNING OUTCOME: LEARNING OUTCOME: Through this activity we have found the height of the pole which cannot be measure directly by measuring tape. ? = 45 ? ? ? = 45 ? = 10 ? 1? ? = 10 ?

ACTIVITY The angle of elevation of a cloud from a point 60 m above a lake is 30 and the angle of depression of the reflection of the cloud in the lake is 60 . Find the height of the cloud from the surface of the lake ANSWER

MIND MAP

INTERESTING FACT: INTERESTING FACT: Did you know? An early application of trigonometry was made by Thales on a visit to Egypt. He was surprised that no one could tell him the height of the 2000 year old Cheops pyramid. He used his knowledge of the relationship between the heights of objects and the length of their shadows to calculate the height for them. This later became the tangent ratio. THALES THE GREAT CHEOPS PYRAMID ***

SUMMARY SUMMARY In this chapter, you have studied the following points : The line drawn from the eye of an observer to a point in the object where the person is viewing is called the line of sight. The angle formed by the line of sight with the horizontal when the object is above the horizontal level is called the angle of elevation. The angle formed by the line of sight with the horizontal when the object is below the horizontal level is called the angle of depression. The height of an object or the distance between distant objects can be determined with the help of trigonometric ratios. ***