Understanding 2-Body Equations of Motion and Solutions
Explore the derivation, assumptions, and solutions to the 2-body equation of motion in physics, along with insights on apogee, perigee, eccentricity, and flight path angles.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
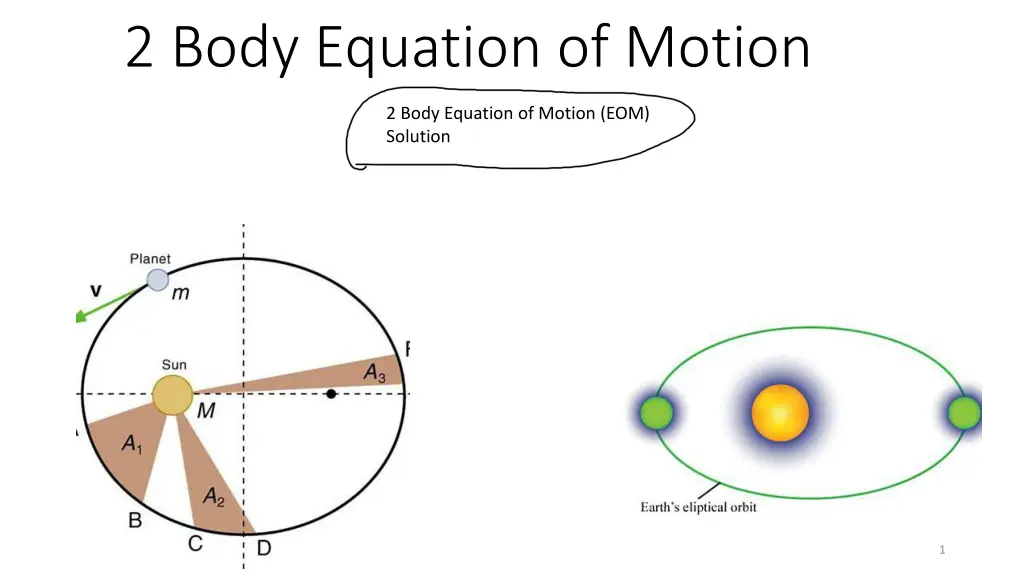
2 Body Equation of Motion 2 Body Equation of Motion (EOM) Solution 1
2 BODY EQUATION OF MOTION (EOM) ? Derivation not shown here ? ?2 ? = 0 ? + ?? ? = position vector ? = ? = velocity vector ? = ? = acceleration vector ? = unit vector in ? direction = G?? Alternate form: ? ? + ?3? = 0 5
ASSUMPTIONS ??
ASSUMPTIONS 1)Only 2 bodies earth and satellite 2)Bodies are spherically symmetrical acts through center of bodies 3) ?? ?? 4) >> any other forces 5) Coordinate system is sufficiently inertial (so Newton s Laws apply) 6) Mass is constant so ? = 0 ?? ?? ?? 7
SOLUTION TO 2 BODY EOM ?(1 ?2) 1 + ???? ? = ? ? ? apogee perigee F F 8 2a
SOLUTION TO 2 BODY EOM ? ? = ? ? a = semi-major axis 2a = ??+ ?? ? apogee perigee Circle: a = R Ellipse: a > 0 Parabola: a = Hyperbola: a < 0 F F = true anomaly 2a Measured from ? ?? ? ?? ?? c 9
SOLUTION TO 2 BODY EOM ? = flight path angle + outward bound (perigee to apogee) - Inbound (apogee to perigee) ? ? apogee perigee e = eccentricity ?? ?? ??+ ?? F F ? = circle: e = 0 ellipse 0 < e < 1 parabola e = 1 hyperbola e > 1 2a ?? ?? c 10
SOLUTION TO 2 BODY EOM y ? = flight path angle ? x apogee perigee F F 2a ?? ?? 11
SOLUTION TO 2 BODY EOM ? c = distance between foci = ?? ??= ?? ? ??= ? ? = ? ?? ? apogee perigee F F ??= ? 1 ? 2a ??= ? + ? = a + ae ?? ?? ??= ?(1 + ?) c 12






















