Understanding Boundary Conditions in Physics
Explore the concept of boundary conditions in physics through a series of equations and descriptions. Delve into symmetric boundary conditions and complete sets of functions, illustrated with helpful images. Uncover the complexities and nuances of these fundamental principles in this detailed analysis.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
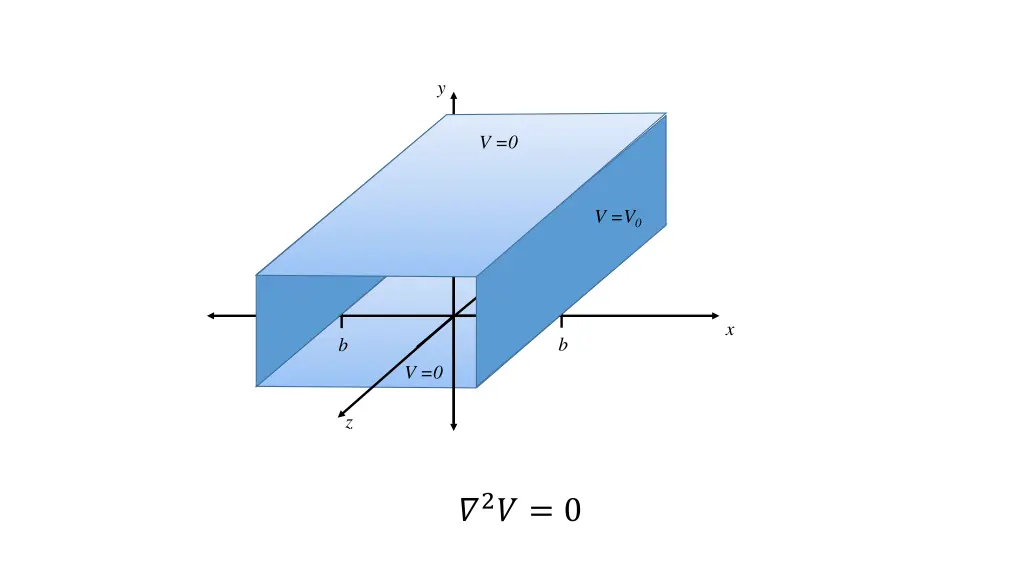
y V =0 a V =V0 x b b V =0 z ?2? = 0
?2? = 0 ?2? ??2 + ?2? ??2 = 0 ? ?,? = ? ? ?(?) ?2(??) ??2 + ?2(??) ??2(?) ??2 + ??2(?) ??2 = 0 ??2(?) ??2 + ??2(?) ??2 = 0 ??2 = 0 ??2(?) ????2 + ??2(?) ????2 = 0 ?2(?) ???2 + ?2(?) ???2 = 0
?2(?) ???2 + ?2(?) ? ? = ????+ ?? ?? ???2 = 0 Y ? = ????(??) + ????(??) ?2(?) ???2 = ?1and ?2(?) ???2 = ?2 ?1= ?2and?2= ?2 Completely general up to this point ?2(?) ???2 = ?2and ?2(?) ???2 = ?2
? ? = ????+ ???? Y ? = ????(??) + ????(??) Boundary conditions Symmetric in x: ? = ? ? ? = ?(???+? ??) ? ? = 2?(???+? ??) = 2?cosh(??) 2 ? ?,? = 2?cosh(??)(???? ?? + ???? ?? ) ? ?,? = cosh(??)(???? ?? + ???? ?? )
? ?,? = cosh(??)(???? ?? + ???? ?? ) ? ?,0 = 0 = cosh(??)(???? 0 + ???? 0 ) ? ?,0 = 0 =???? 0 ) ? ?,? = ?cosh(??)??? ?? ? ?,? = 0 = ?cosh(??)??? ?? ?? = ?? ? ?,? = ?cosh(???/?)??? ???/?
? ?,? = ?cosh(???/?)??? ???/? ? = 0,1,2,3 15 10 5 0 -5 150 150 100 100 50 50 0 0 One boundary condition to go
? ?,? = ?cosh(???/?)??? ???/? 15 10 5 ? = 0,1,2,3 0 -5 150 150 100 100 ? ?,? = ?0= ?cosh(???/?)??? ???/? Never going to happen 50 50 0 0 ? ?,? = ??cosh(???/?)??? ???/? ? ?,? = ??cosh(???/?)??? ???/? ?=1 ? ?,? = ?0= ??cosh(???/?)??? ???/? ?=1
?0= ??cosh(???/?)??? ???/? ?=1 15 10 5 0 -5 150 150 100 100 50 50 0 0
?0= ??cosh(???/?)??? ???/? ?=1 ?0??? ? ??/? = ??cosh(???/?)??? ???/? ??? ? ??/? ?=1 ? ? ?0??? ? ??/? ?? = ??cosh(???/?)??? ???/? ??? ? ??/? ?? ?=1 0 0 ? ? ?0??? ? ??/? ?? = ??? ???/? ??? ? ??/? ?? ??cosh(???/?) ?=1 0 0
? ? ?0??? ? ??/? ?? = ??? ???/? ??? ? ??/? ?? ??cosh(???/?) ?=1 0 0 ? ??? ???/? ??? ? ??/? ?? = 0 ??? ? ? 0 =? 2??? ? = ? Orthogonal, complete set of functions
? ? ?0??? ? ??/? ?? = ??? ???/? ??? ? ??/? ?? ??cosh(???/?) ?=1 0 0 ? ??? ???/? ??? ? ??/? ?? = 0 ??? ? ? 0 =? 2??? ? = ? ? ?0??? ? ??/? ?? = ?? cosh(? ??/?)? 2 ? 0 ?0??? ? ??/? ?? = ??cosh(? ??/?)? 2 0 ? ? =2??0 ?? ?0??? ? ??/? ?? = ?0 ??? ? ??/? ?? = 0 ?? ? ?? ???? ?? ? ?? ??? 0 0
? ?0??? ? ??/? ?? = ??cosh(? ??/?)? 2 0 2??0 ??? ? ? 2 ??? ??? ? = ??cosh ?? 4?0/?? cosh(???/?) ??= ? ?,? = ??cosh(???/?)??? ???/? ?=1,3,5 4?0 ?? cosh(???/?) cosh(???/?)sin(???/?) ? ?,? = ?=1,3,5
4?0 ?? cosh(???/?) cosh(???/?)sin(???/?) ? ?,? = ?=1,3,5 15 10 5 4?0 ? cosh(??/?) cosh(??/?)sin(??/?) 0 -5 150 150 100 100 50 50 0 0 15 10 4?0 ? cosh(??/?) cosh(??/?)sin(??/?) +4?0 cosh(3??/?) cosh(3??/?)sin(3??/?) 5 0 3? -5 150 150 100 100 50 50 0 0
