Understanding Byzantine Agreement in Distributed Systems

CS6410 Byzantine Agreement Kai Sun *Some slides are borrowed from Ken Birman, Andrea C. Arpaci- Dusseau, Eleanor Birrell, Zhiyuan Teo, and Indranil Gupta

So Far Weve Talked About State machine replication Paxos

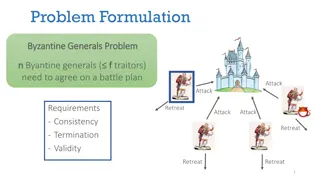
So Far Weve Talked About Assumption Processors do not collude, lie, or otherwise attempt to subvert the protocol But what if the assumption does not hold?

The Byzantine Generals Problem Leslie Lamport PhD Brandeis 1972 LaTeX, Clocks, Paxos, Robert Shostak PhD Harvard 1974 Staff scientist for SRI International Founder and vice president of software for Ansa Software Founder and CTO for Portera Founder and CTO for Vocera Marshall Pease

The Byzantine Generals Problem I have long felt that, because it was posed as a cute problem about philosophers seated around a table, Dijkstra's dining philosopher's problem received much more attention than it deserves. * Leslie Lamport *http://research.microsoft.com/en-us/um/people/lamport/pubs/pubs.html

Byzantine Agreement General commands soldiers If all loyal soldiers attack victory is certain If none attack, the Empire survives If some attack, the Empire is lost Gong keeps time But they don t need to all attack at once Curses! I m surrounded! Attack!

Byzantine Soldiers The enemy works by corrupting the soldiers Orders are distributed by exchange of messages Corrupt soldiers violate protocol at will Corrupt soldiers can t intercept and modify messages between loyal troops The gong sounds slowly There is ample time for loyal soldiers to exchange messages (all to all)

More Formal A commander must send an order to his ? 1 lieutenants such that IC1. All loyal lieutenants obey the same order IC2. If the commander is loyal, then every loyal lieutenant obeys the order he sends IC1 and IC2 are called the interactive consistency conditions.

Impossibility Results Let?be the maximum number of faulty processes that our protocol is supposed to tolerate Byzantine agreement is not possible with fewer than 3? + 1processes

Impossibility Result With only 3 generals, no solution can work with even 1 traitor (given oral messages) commander attack L1 L2 retreat What should lieutenant 1 (L1) do? Is commander or lieutenant 2 (L2) the traitor?

Option 1: Loyal Commander commander attack attack L1 L2 retreat What must L1 do? By IC2: L1 must obey commander and attack

Option 2: Loyal L2 commander retreat attack L1 L2 retreat What must L1 do? By IC1: L1 and L2 must obey same order --> L1 must retreat

Two Options commander commander attack retreat attack attack L1 L1 L2 L2 retreat retreat Problem: L1 can t distinguish between 2 scenarios

General Impossibility Result No solution with fewer than 3m+1 generals can cope with m traitors < see paper for details >

Oral Messages Assumptions A1) Every message sent is delivered correctly No message loss A2) Receiver knows who sent message Completely connected network with reliable links A3) Absence of message can be detected Synchronous system only

Oral Message Algorithm OM(0) Commander sends his value to every lieutenant Each lieutenant uses the value received from the commander, or uses the value RETREAT if he receives no value

Oral Message Algorithm OM(m), m>0 Commander sends his value to every lieutenant For each ?, let ?? be value Lieutenant ? receives from commander (or RETREAT if he receives no value) Act as commander for OM(m-1) and send ?? to n-2 other lieutenants For each ? and each ? ?, let ?? be value Li. ? received from Li. ? in the above step (or RETREAT if he received no such value). Li. ? computes majority(?1,...,?? 1)

Example: Bad Lieutenant Scenario: m=1, n=4, traitor = L3 C Round 0 A A A L2 L3 L1 C A A A A Round 1 A A L2 L3 L1 R A R Decision L1 = majority(A, A, R); L2 = majority(A, A, R); Both attack!

Example: Bad Commander Scenario: m=1, n=4, traitor = C C A A Round 0 R L2 L3 L1 C A A R A Round 1 R A L2 L3 L1 A R A Decision L1=majority(A, R, A); L2=majority(A, R, A); L3=majority(A,R,A); Attack!

Bigger Example: Bad Lieutenants Scenario: m=2, n=3m+1=7, traitors=L5, L6 C A A A A A A L3 L6 L1 L2 L4 L5 Messages? L3 L6 L1 L2 L4 L5 A R A A A R majority(A,A,A,A,R,R) ==> All loyal lieutenants attack! Decision?

Bigger Example: Bad Commander+Lieutenant Scenario: m=2, n=7, traitors=C, L6 C A x A R R A L3 L6 L1 L2 L4 L5 Messages? L3 L6 L1 L2 L4 L5 A A R R A A,R,A,R,A Decision?

Decision with Bad Commander+Lieutenant L1: majority(A,R,A,R,A,A) ==> Attack L2: majority(A,R,A,R,A,R) ==> Retreat L3: majority(A,R,A,R,A,A) ==> Attack L4: majority(A,R,A,R,A,R) ==> Retreat L5: majority(A,R,A,R,A,A) ==> Attack Problem: All loyal lieutenants do NOT choose the same action

Next Step of Algorithm Verify that lieutenants tell each other the same thing Requires ? + 1 rounds What messages does L1 receive in this example? Round 0: A Round 1: 2R, 3A, 4R, 5A, 6A (doesn t know 6 is traitor) Round 2: 2 { 3A, 4R, 5A, 6R} 3 {2R, 4R, 5A, 6A} 4 {2R, 3A, 5A, 6R} 5 {2R, 3A, 4R, 6A} 6 { ?, ?, ?, ? } All see same messages in round 2 from L1, L2, L3, L4, and L5 majority(A,R,A,R,A,-) ==> All attack C A x A R R A L3 L6 L1 L2 L4 L5 Messages? L3 L6 L1 L2 L4 L5 A A R R A A,R,A,R,A

Algorithm Complexity What s the cost? OM(m) invokes (n-1) OM(m-1). OM(m-1) invokes (n-2) OM(n-2). OM(m-k) will be called (n-1)(n-2) (n-k) times. Algorithm complexity is O(nm). (note: m = number of failures)

Signed Messages Problem Traitors can lie about what others said How can we remove that ability?

Signed Messages New assumption (A4) -- Signed messages (Cryptography) Loyal general s signature cannot be forged and contents cannot be altered Anyone can verify authenticity of signature Simplifies problem: When Li. ? passes on signed message from ?, receiver knows that ?didn t lie about what j said Lieutenants cannot do any harm alone (cannot forge loyal general s orders) Only have to check for traitor commander With cryptographic primitives, can implement Byzantine Agreement with m+2 nodes, using SM(m)

Signed Messages Algorithm: SM(m) Initially ??= Commander signs ? and sends to all as (?:0) Each Li. ?: A) If receive (?:0) and no other order 1) ?? = {?} 2) Send (?:0:?) to all B) If receive (?:0:?1:...:??) and ? not in ?? 1) Add ? to ?? 2) If (?<m) send (?:0:?1:...:??:?) to all not in ?1 ?? 4. When no more messages, obey order of choice(??) 1. 2. 3.

Signed Messages Algorithm: SM(m) ? ????(?) If the set ? consists of the single element ?, then ? ????(?) = ? ? ???? =RETREAT One possible definition is to let ? ????(?) be the median element of ?

SM(1) Example: Bad Commander Scenario: m=1, n=m+2=3, bad commander C A:0 R:0 L2 L1 What next? A:0:L1 L2 L1 R:0:L2 ?1={A,R} ?2={R,A} Both apply same decision to {A,R}

SM(2): Bad Commander+Lieutenant Scenario: m=2, n=m+2=4, bad commander and L3 Goal? L1 and L2 must make same decision C A:0 x A:0 L2 L3 L1 A:0:L1 A:0:L3 R:0:L3:L1 L3 L2 L1 A:0:L2 L2 L1 R:0:L3 ?1 = ?2 = {A,R} ==> Same decision

Other Variations How to handle missing communication paths < see paper for details >

Compared with Asynchronous Scenarios m = traitors n = total Synchronous Asynchronous n <= 3m m >=1 * Oral messages: fails if n >= 3m+1 no guarantee works if m >= 1 * won t fail unless no correct processes Signed messages: fails if n >= 1 no guarantee works if *Fischer, Michael J., Nancy A. Lynch, and Michael S. Paterson. "Impossibility of distributed consensus with one faulty process." Journal of the ACM (JACM) 32.2 (1985): 374-382.

Thought?

Easy Impossibility Proofs for Distributed Consensus Problems Michael J. Fischer PhD from Harvard (applied mathematics) Professor at Yale ACM Fellow Nancy A. Lynch PhD from MIT Professor at MIT ACM Fellow, Dijkstra Prize, Knuth Prize, Michael Merritt PhD from GeTech President, Brookside Engine Company No. 1. Vice-Chair, Advancement Committee, Patriots' Path Council

Easy Impossibility Proofs for Distributed Consensus Problems A process is regarded as a machine processing a tape of inputs Called an agreement device They build a communications graph. The messages that pass over an edge from a source to a destination node are a behavior of the device on that edge Behavior of the system is a set of node and edge behaviors In their proofs, faulty devices often exhibit different and inconsistent behaviors with respect to different participants

Locality An axiom of this model Basically says that the way a node will behave is completely determined by the inputs it starts with and that it receives on incoming edges Fault axiom: a faulty device can mimic behavior of any correct device in any run. At the receiving end of an edge from it, the receiver can t distinguish the faulty device from the device it mimics.

How They Prove the 3t+1 Bound Start by assuming that the consensus problem can be solved; for 3 processes the system looks like this: A B C

Now Build a Covering Graph Looks like the original graph G each node is attached to two others by edges Also assign initial input values as shown A0 C1 A B0 B1 C0 A1 B C

Now Focus on a First Scenario Consider B0 and C0 in a run where A is faulty A0 F C1 B0 B1 C0 A1 B0 C0

By Assumption They Reach Agreement In particular, they reach agreement if F mimics what A0 would have done on the edge (A,B) and what A1 would have done on the edge (A,C) By the validity requirement, B and C must chose 0 So A0 and A1 both pick 0 too, with these inputs

Consider a Second Scenario Consider A1 and C0 in a run where B is faulty A0 A1 C1 B0 B1 C0 A1 F C0

Causing Trouble Suppose that F mimics B0 when talking to C This is indistinguishable to C from the initial scenario So C will need to decide 0 By agreement, A also decides 0

Consider a Final Scenario Consider A1 and B1 in a run where C is faulty A0 A1 C1 B0 B1 C0 A1 B1 F

Force a Contradiction Now we have the original setup with inputs 1 Validity requirements force a decision value of 1 But the edge behaviors for A are actually identical in the 2nd and 3rd scenarios! We ve shown that a single device, presented with identical inputs, would pick different values A contradiction

Generalize to Arbitrary Number of Nodes They partition the nodes into three groups, A, B and C, with at least 1 and at most 1/3 of the nodes in each group They treat all the nodes in group A the way that we treated device A in our 3-node case, and similarly for B and C Same argument again leads to contradiction

Other Byzantine Impossibility Result Connectivity: 2t+1 connectivity required to achieve Byzantine agreement

Thought?

The End