Understanding Center of Gravity and Centroids in Physics

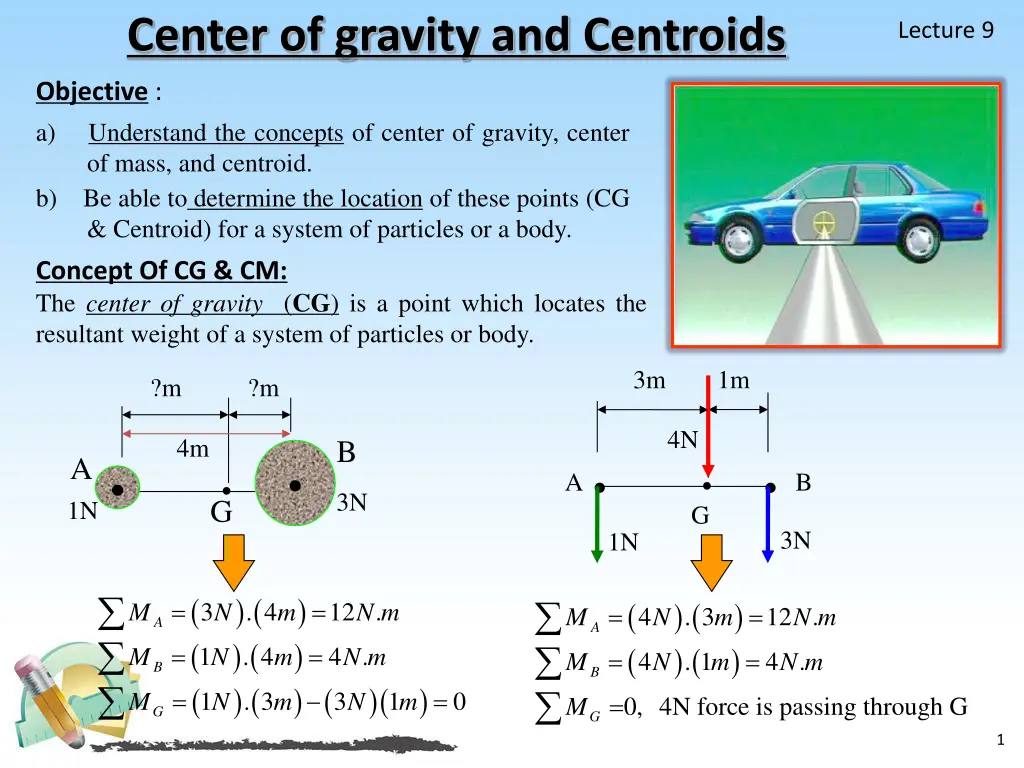
Center of gravity and Centroids Lecture 9 Objective : a) Understand the concepts of center of gravity, center of mass, and centroid. b) Be able to determine the location of these points (CG & Centroid) for a system of particles or a body. Concept Of CG & CM: The center of gravity (CG) is a point which locates the resultant weight of a system of particles or body. 3m 1m ?m ?m 4N 4m B A 1N A B 3N G G 3N 1N ( ( ( ) ( ) ( ) ( . 3 ) ) ) ( ( ( 0, 4N force is passing through G ) ( ) ( . 1 ) ) = = 3 . 4 12 . M N m N m = = 4 . 3 12 . M N m N m A A = = 1 . 4 4 . N m M N m = = 4 4 . N m M N m B B )( ) = = 1 3 1 0 M N m N m = M G G 1

Lecture 9 Concept Of CG & CM: Hence, from the definition of a resultant force, the sum of moments due to individual particle weight about any point is the same as the moment due to the resultant weight located at G. Also, note that the sum of moments due to the individual particle s weights about point G is equal to zero. Similarly, the center of mass is a point which locates the resultant mass of a system of particles or body. Generally, its location is the same as that of G. Centroid: The Centroid is a point defines the geometric center of an object. If the material composing a body is uniform or homogeneous, the density or specific weight will be constant throughout the body, then the centroid is the same as the center of gravity or center of mass. centroid Sometimes located outside the body! If an object has an axis of symmetry, then the centroid of object lies on that axis. the is 2

Lecture 9 Difference between Center of Area and Center of Mass: To understand the difference between Center of Area and Center of Mass: If we have two object having the same shape, weight and mass, these objects, then have the same center of area and center of mass. By sticking another object have a weight on this surface as shown in the figure. Then the center of mass will be changed, but the center of area will still the same. Applications: Cars, trucks, bikes, etc., are assembled using many individual components. When designing for stability on the road, it is important to know the location of the bikes center of gravity (CG). Should (CG) be higher or lower for making the bikes more stable? If we know the weight and CG of individual components, how can we determine the location of the CG of the assembled unit? 3

Lecture 9 APPLICATIONS The I-beam is commonly used in building structures. When doing a stress analysis on an I - beam, the location of the centroid is very important. How can we easily determine the location of the centroid for a given beam shape? CONCEPT OF A COMPOSITE BODY Many industrial objects can be considered as composite bodies made up of a series of connected simpler shaped parts or holes, like a rectangle, triangle, and semicircle. Knowing the location of the centroid, C, or center of gravity, G, of the simpler shaped parts, we can easily determine the location of the C or G for the more complex composite body. This can be done by considering each part as a particle and following the procedure as described later. This is a simple, effective, and practical method of determining the location of the centroid or center of gravity. 4

CG / CM FOR A SYSTEM OF PARTICLES Consider a system of n particles as shown in the figure. The net or the resultant weight is given as: WR= W Summing the moments about the y-axis, we get: x WR= x1W1+ x2W2+ .. + xnWn Where: x1represents x coordinate of W1, etc.. Similarly, we can sum moments about the x- and z-axes to find the coordinates of ( CG ). Lecture 9 ~ A rigid body can be considered as made up of an infinite number of particles. Using the same principles, we get the coordinates of ( CG ) by simply replacing the discrete summation sign ( ) by the continuous summation sign ( ) and (W) by (dW). Similarly, the coordinates of the center of mass and the centroid of volume, area, or length can be obtained by replacing W by M, V,A, or L, respectively. 5

Lecture 9 STEPS FOR DETERMING AREA CENTROID ( First Moment of Area ) 1. Choose an appropriate differential element ( dA ) at a general point ( x, y ). Hint: Generally, if ( y ) is easily expressed in terms of ( x ) ( e.g., y = 15 x2 ), use a vertical rectangular element. If the converse is true, then use a horizontal rectangular element. 2. Express ( dA ) in terms of the differentiating element ( dx ) (or dy). 3. Determine coordinates ( x , y ) of the centroid of the rectangular element in terms of the general point ( x, y ). ~ ~ Where: = the distance between center of area to ( y ) axis = the distance between center of area to ( x ) axis 4. Express all the variables and integral limits in the formula using either ( x or y ) depending on whether the differential element is in terms of ( dx or dy ), respectively, and integrate. y is expressed in terms of x Consider a vertical element xdA ydA = = , x y dA dA x is expressed in terms of y Consider a horizontal element 6

Lecture 9 Centroids of common shapes C C h h h / 2 h / 3 b / 3 b / 2 b b c = 0 x = + 4 ( ) r x b c 4 r 1 = = = x y 3 y 3 2 3 = y h 1 3 = = 2 A r A r 1 1 = A b h 1 4 2 2 = + = + 2 ( r ) P 2 ( r ) P 1 7 2

Lecture 9 Example 1: Find the centroid location (x , y) for the shaded area: Solution 1. Since y is given in terms of ( x ), choose ( dA ) as a vertical rectangular strip. 2. dA = y . dx ~ = (9 x2) . dx ~ 3. x = x 4. x = ( Ax dA) / ( AdA) 3 and y = y / 2 ~ 0 x . ( 9 x2 ) d x 0 ( 9 x2 ) d x = [ 9 ( 9 ) / 2 81 / 4 ] / [ 9 ( 3 ) ( 27 / 3 ) ] = 1.13 ft [ 9 ( x2 ) / 2 ( x4 ) / 4] 3 0 = = x, y 3 [ 9 x (x3 ) / 3 ] 3 x , y~ ~ 0 3 ~ Ay dA AdA 0 ( 9 x2 ) ( 9 x2 ) dx 3 = y = = 3.60 ft 0 ( 9 x2 ) d x 8

Lecture 9 Example 2: Find the ( x ) of the centroid for the shaded area: Solution 1. Choose ( dA ) as a horizontal rectangular strip. 2. dA = ( x2 x1) dy = [ (2 y) y2 ] . dy x = ( x1+ x2) / 2 = 0.5 [ ( 2 y) + y2] x = ( Ax dA) / ( AdA) AdA =0 ( 2 y y2 ) . dy = [ 2 y y2/ 2 y3/ 3] 1= 1.167 m2 1 ~ 3. ~ 4. X 1 0 Ax dA = 0 0.5 ( 2 y + y2) ( 2 y y2) dy = 0.5 0 ( 4 4 y + y2 y4) dy = 0.5 [ 4 y 4 y2/ 2 + y3/ 3 y5/ 5 ] 1= 1.067 m3 1 0 x = 1.067 / 1.167 = 0.914 m 9

Lecture 9 Example 3: Find the centroid location (x , y) for the part with shaded area: Solution: 1. This body can be divided into the following pieces: rectangle (a) + triangle (b) + quarter circular (c) semicircular area (d) 2. Make up the table using parts a, b, c, and d. Area A (in2) x y A x ( in3) A y ( in3) Segment (in) (in) Rectangle Triangle Q. Circle Semi-Circle 3. Start to fill the table using the data given for each parts a, b, c, and d, let take for example part ( a ) the rectangular: The rectangular area ( A ) = 3 * 6 = 18 in2 x = 6 / 2 = 3 in , y = 3 / 2 = 1.5 in 10

Lecture 9 Continue of Example 3: A . x = 18 * 3 = 54 in2, . A . y = 18 * 1.5 = 27 in y = 1 in Same step for the triangular: The triangular area ( A ) = 3 * 3 / 2 = 4.5 in2 6 in x 1 in x = ( 3 / 3 ) + 6 = 7 in , y = 3 / 3 = 1 in A . x = 4.5 * 7 = 31.5 in2, A . y = 4.5 * 1 = 4.5 in Do the same step for the other shapes to obtain the following table: Area A (in2) x y A x ( in3) A y ( in3) Segment (in) (in) Rectangle Triangle Q. Circle Semi-Circle 1.5 1 27 4.5 9 - 2/3 18 4.5 3 7 54 31.5 9 0 4(3) / (3 ) 4(1) / (3 ) 9 / 4 / 2 4(3) / (3 ) 0 28.0 76.5 39.83 11

Lecture 9 Continue of Example 3: 4. Use the table data and these formulas to find the coordinates of the centroid. = C x = ( x A) / ( A ) = 76.5 in3/ 28.0 in2= 2.73 in y = ( y A) / ( A ) = 39.83 in3/ 28.0 in2= 1.42 in 12