Understanding Circle Theorems and Geometric Properties
Explore circle theorems, geometric properties, and angle relationships in circles. Learn about tangents, chords, arcs, sectors, and more in this comprehensive guide with detailed explanations and diagrams.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
03 June 2025 Circle theorems: The angle in the alternate segment LO: To solve problems using circle theorems. www.mathssupport.org
Naming the parts of a circle A circle is a set of points equidistant from a fixed point called the centre. The distance around the entire circle boundary is called the circumference. The radius is any line segment joining its centre to any point on the circumference. radius centre The diameter is a line segment passing through the centre. Note that the diameter of a circle is twice its radius circumference www.mathssupport.org
Naming the parts of a circle A chord is any line segment that joins two points on the circle. Therefore, a diameter is an example of a chord. It is the longest possible chord. The line that touches the circumference in exactly one point is called a tangent or a tangent line. The point where the tangent touches the circle is called the point of contact or point of tangency. centre www.mathssupport.org
Naming the parts of a circle The region of a circle enclosed by a chord and an arc a Segment is called Any chord encloses two segments, which have different areas. If the segment is enclosed by the diameter a semicircle Major segment it is called Minor segment www.mathssupport.org
Arcs and sectors arc An arc is any continuous part of the circumference. sector When an arc is bounded by two radii a sector is formed. www.mathssupport.org
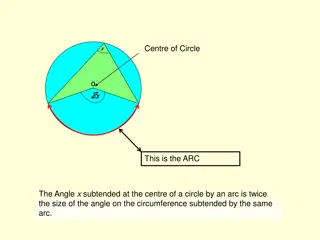
The angle in the alternate segment Draw a circle, label the centre O Choose a point A on the circumference. Draw a tangent line PQ that touches the circumference at A Choose another point B on the circumference. Draw a chord from A, to the point B, Measure the angle BAQ, C Choose another point C on the opposite segment of the circumference. Draw a line from A, to the point C, Draw a line from B, to the point C, Measure the angle ACB, What do you notice? Measure the angle PAC, x O B y Q x y Angle BAQ = ACB Measure the angle ABC, Angle PAC = ABC P A What do you notice? Statement The angle between a tangent and a chord is equal to the angle in the alternate segment. www.mathssupport.org
The angle in the alternate segment We have just seen a demonstration that shows that the angle between a tangent and a chord is equal to the angle in the alternate segment We can prove that = as follows: Draw the lines OA, and OB. (both radii) OA = OB. C OAB = OBA (opposite to equal sides) OAQ = 90 So, O B = 90 = OBA (angle between radius and tangent) O B 2 (angles at the base of an isosceles triangle) = 180 2(90 ) AOB (sum of the angles in a triangle) Q P = 180 180 + 2 AOB= 2 AOB = 2( ACB) 2 = 2 = A angle at the centre is double the angle at the circumference www.mathssupport.org
The angle in the alternate segment Calculate the size of the angles a and b in the triangle: b = 68 (the angle in the alternate segment) 52 a = 180 (52 + 68 ) = 60 (angles in a triangle) 68 a b www.mathssupport.org
The angle in the alternate segment A, B, and C are points on a circle. DCE is a tangent on a circle at C. Angle ACD = 53 and angle BCE = 61 . Write down the size of angle ABC. Write down the size of angle BAC. B E 61 ABC = 53 (the angle in the alternate segment) C BAC = 61 (the angle in the alternate segment) 53 A D www.mathssupport.org
The angle in the alternate segment AB is tangent to the circle at C. Find x D ECA = x alternate angles x EDC = x Angle in the alternate segment B 180 = 40 + x + x (angles in a triangle) 140 = 2x 40 x C x E x = 70 A www.mathssupport.org
Thank you for using resources from A close up of a cage Description automatically generated For more resources visit our website https://www.mathssupport.org If you have a special request, drop us an email info@mathssupport.org Get 20% off in your next purchase from our website, just use this code when checkout: MSUPPORT_20 www.mathssupport.org