Understanding Complex Numbers: Rectangular vs. Exponential Forms
Explore the concepts of complex numbers in both rectangular and exponential forms, understanding the real and imaginary parts, their relationships, and the geometry that relates the forms using trigonometry. Dive into the quadrants and mathematical relationships between the forms to enhance your understanding of complex numbers.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
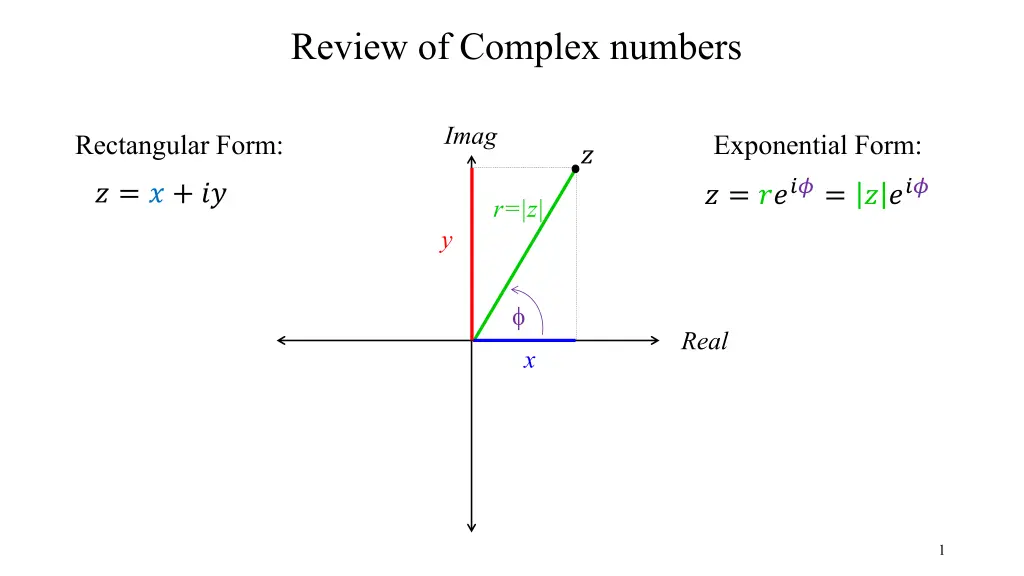
Review of Complex numbers Imag Rectangular Form: Exponential Form: ? ? = ????= ? ??? ? = ? + ?? r=|z| y Real x 1
Real & Imaginary Parts of Rectangular Form Imag The real and imaginary parts of a complex number in rectangular form are real numbers: ? ?? ? = ? y=Im(z) ?? ? = ? Therefore, rectangular form can be equivalently written as: Real x=Re(z) ? + ?? = ?? ? + ???(?)
Geometry Relating the Forms The real and imaginary components of exponential form can be found using trigonometry: Imag ? cos? =??? ??=? r=|z| ? = ?cos? ? Real x Imag ? sin? =??? ??=? r=|z| ? = ?sin? ? y Real
Geometry Relating the Forms: Real & Imaginary Parts The real and imaginary parts of a complex number can be expressed as follows: Imag ? ?? ? = ?= ?cos? = ? cos? r=|z| ? = ?? ? = ?sin? ?? ? = ? = ?sin? = ? sin? ? Real ? = ?? ? = ?cos?
Geometry Relating the Forms: Quadrants In exponential form, the positive angle, ?, is always defined from the positive real axis. If the complex number is not in the first quadrant, then the triangle has lengths which are negative numbers. Imag Imag cos? =??? ??=|?| ? ? ? > 0 ? > 0 r=|z| ? < 0 ? > 0 y ? = ?cos? = ?cos? Real ? < 0 ? < 0 ? > 0 ? < 0 ? Real x
Geometry Relating the Forms: ? in terms of ? and ? Imag Use Pythagorean Theorem ? ?2= ?2= ?2+ ?2 r=|z| y to find ? in terms of ? and ?: ?2+ ?2 ? = ?= Real x
Geometry Relating the Forms: ? in terms of ? and ? Use trigonometry hyp opp ??? ??? tan? = ? to find ? in terms of ? and ?: adj Imag ? tan? =?sin? ?cos?=??(?) ??(?)=? r=|z| ? y ? = tan 1? ? Real x
Summary of Algebraic Relationships between Forms Imag ? ? = ?cos? r=|z| y ? = ?sin? ?2+ ?2 ? = ?= Real x ? = tan 1? ?
Eulers Formula ???= cos? + ?sin?
Consistency argument ? = ????= |?|??? ? = ? + ?? If these represent the same thing, then the assumed Euler relationship says: ? = ? + ?? Rectangular Form: = ?cos? + ??sin? = ? cos? + ? ? sin? = ?(cos? + ?sin?) = ? (cos? + ?sin?) = ????= |?|??? Exponential Form:
Eulers Formula ???= exp(??) = cos? + ?sin? Can be used with functions: ???0?= exp(??0?) = cos?0? + ?sin?0? 11
Addition & Subtraction of Complex Numbers Addition and subtraction of complex numbers is easy in rectangular form ?1= ? + ?? ? = ?1+ ?2= ? + ??+ ? + ?? = (? + ?) + ?(? + ?) Imag Addition and subtraction are analogous to vector addition and subtraction ?1 = ? ? + ? ? ?2 = ? ? + ? ? ?2= ? + ?? ? = ?1+ ?2 = ? + ? ? + (? + ?) ? y ?1 ?1 b a b a x c ?2 ? Real c d ? d ?1 ?2 12
Multiplication of Complex Numbers Multiplication of complex numbers is easy in exponential form Multiplication by a complex number, ?????, can be thought of as scaling by ?and rotation by ? ?2= ?2??? ?1= ?1??? Imag ????? ? = ?1?2= ?1????2??? = ?1?2??(?+?) = |?1||?2|??(?+?) Angle rotated counterclockwise by ? ? ? Magnitude scaled by ? Real 13
Division of Complex Numbers Division of complex numbers is easy in exponential form ?1= ?1??? Division of complex numbers is sometimes easy in rectangular form ? =? + ?? ? + ?? =? + ?? ? + ?? ? ?? ?2= ?2??? ?2 =?1??? =?1 ? =?1 ? ?? ?2??? Multiply by 1 using the complex conjugate of the denominator ?2??(? ?) =|?1| |?2|??(? ?) = |?|??(? ?) =?? + ?? + ?(?? ??) ?2+ ?2 =?? + ?? ?2+ ?2+ ?(?? ??) ?2 ?2 = ??(?) + ???(?) 14
Complex Conjugate Another important idea is the COMPLEX CONJUGATE of a complex number. To form the c.c.: change i -i Imag ? r=|z| ? = ???? ? = ?? ?? ? = ? + ?? ? = ? ?? y Real x The complex conjugate is a reflection about the real axis ?
Common Operations with the Complex Conjugate Addition of the complex number and its complex conjugate results in a real number ? + ? = ? + ?? + ? ?? = 2? Imag ? r=|z| y The product of a complex number and its complex conjugate is REAL. Real x ? + ? = 2x ?? = ?????? ?? = ?2??(? ?) = ?2 ? = |?|2
