Understanding Electric Field Lines, Flux, and Gauss's Law
Explore the concepts of electric field lines, electric flux, and Gauss's law in electrostatics. Learn about the properties of electric field lines, the calculation of electric flux, and the application of Gauss's law to determine electric fields due to different charge distributions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Chapter 1: Electrostatics: Introduction: Electric field lines, electric flux and Gauss law. The divergence of E, Curl of E, Application of Gauss law: i)Electric field due to a uniform charged sphere ii)Electric field due to charged cylinder, Gaussian pillbox, Poisson s equation, Uniqueness theorem (First and Second). equation, Laplace s
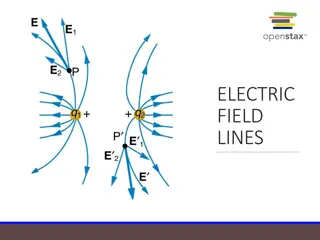
Electric field line:- An electric field line is an imaginary line or curve drawn through a region of empty space so that its tangent at any point is in the direction of the electric field vector at that point. The relative closeness of the lines at some place gives an idea about the intensity of electric field at that point.
You can feel the attraction between unlike charges and the repulsion between like charges as though they are trying to push each other away.
Properties of Electric Field Lines The start point of the field lines is at the positive charge and end at the negative charge. The field lines never intersect each other. The field lines are perpendicular to the surface of the charge. The magnitude of charge and the number of field lines, both are proportional to each other. When the field is stronger, the field lines are closer to each other Electric field and electric field lines are tangent at the point where they pass through.
Electric flux:- Electric flux is the rate of flow of the electric field through a given area. Electric flux is proportional to the number of electric field lines going through avirtual surface. The total number of electric field lines passing a given area in a unit time is defined as the electric flux. Electric flux is a scalar quantity and is denoted by .
If the electric field is uniform, the electric flux passing through a surface of vector area S is E=E S=EScos where E is the magnitude of the electric field (having units of V/m), S is the area of the surface, and is the angle between the electric field lines and the normal to S.
Gausss law:- Gauss s law states that the electric flux through any closed surface is proportional to the total electric charge enclosed by this surface.
Gausss law for the electric field describes the static electric field generated by a distribution of electric charges. By convention, a positive electric charge generates a positive electric field. The law was published in 1867 by the famous German mathematician Carl Friedrich Gauss.
Gausss law in integral form is given below: E dA=Q/ 0 .. (1) Where, E- is the electric field vector Q- is the enclosed electric charge 0-is the electric permittivity of free space A -is the outward pointing normal areavector. Flux is a measure of the strength of a field passing through a surface. Electric flux is defined as = E dA . (2)