Understanding Fractions: Definition, Types, and Properties

StudyMafia.Org Fractions Submitted To: Submitted By: Studymafia.org Studymafia.org

Table Contents Definition Introduction Parts of Fraction Types of Fractions Properties of Fraction Rules for Fraction Conclusion 2

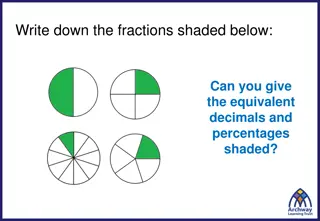
Definition In Mathematics, fractions are represented as a numerical value, which defines a part of a whole. 3

Introduction A fraction shows part of a whole. This whole can be a region or a collection. The word fraction is derived from the Latin word "fractio" which means 'to break'. The Egyptians, being the earliest civilization to study fractions, used fractions to resolve their mathematical problems, which included the division of food, supplies, and the absence of a bullion currency. 4

5

Parts of Fractions The denominator indicates the number of parts in which the whole has been divided into. It is placed in the lower part of the fraction below the fractional bar. 6

Parts of Fractions The numerator indicates how many sections of the fraction are represented or selected. It is placed in the upper part of the fraction above the fractional bar. 7

Types of Fractions Proper Fraction Proper fractions are the fractions in which the numerator is less than its denominator. For example, 5/7, 3/8, 2/5, and so on are proper fractions. 8

Types of Fractions Improper Fraction An improper fraction is the type of fraction in which the numerator is more than or equal to its denominator. It is always the same or greater than the whole. For example, 4/3, 5/2, 8/5, and so on. 9

Types of Fractions Unit Fraction Fractions in which the numerator is 1 are known as unit fractions. For example, 1/4, 1/7, 1/9, and so on. Mixed Fraction A mixed fraction is a mixture of a whole number and a proper fraction. 10

Types of Fractions Like and Unlike Fractions Like fractions are the fractions that have the same denominators. For example, 5/15, 3/15, 17/15, and 31/15 are like fractions. Unlike fractions are the fractions which have different denominators. For example, 2/7, 9/11, 3/13, and 39/46 are unlike fractions. 11

Types of Fractions Equivalent Fraction Equivalent fractions are the fractions that represent the same value after they are simplified. To get equivalent fractions of any given fraction: We can multiply both the numerator and the denominator of the given fraction by the same number. We can divide both the numerator and the denominator of the given fraction by the same number. 12

Properties of Fractions Commutative and associative properties hold true for fractional addition and multiplication The identity element of fractional addition is 0, and fractional multiplication is 1 The multiplicative inverse of a/b is b/a, where a and b should be non zero elements Fractional numbers obey the distributive property of multiplication over addition 13

Rules for Fractions Rule #1: Before adding or subtracting fractions, we should make sure that the denominators are equal. Hence, the addition and subtraction of fractions are possible with a common denominator. 14

Rules for Fractions Rule #2: When we multiply two fractions, then the numerators are multiplied as well as the denominators are multiplied. Later simplify the fraction. 15

Rules for Fractions Rule #3: When we divide a fraction from another fraction, we have to find the reciprocal of another fraction and then multiply with the first one to get the answer. 16

Conclusion Fractions are the numerical values that are a part of the whole. A whole can be an object or a group of objects. If a number or a thing is divided into equal parts, then each part will be a fraction of the whole. A fraction is denoted as a/b, where a is the numerator and b is the denominator. 17

References Google.com Wikipedia.org Studymafia.org Slidespanda.com

Thanks To StudyMafia.org