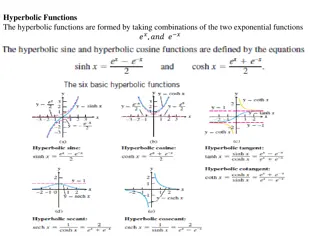
Understanding Functions and Relationships in Mathematics
Explore various mathematical concepts such as one-to-one relationships, many-to-many relationships, many-to-one relationships, as well as functions and composite functions through illustrative examples and diagrams. Delve into the world of functions and relationships in mathematics to deepen your understanding of these fundamental concepts.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
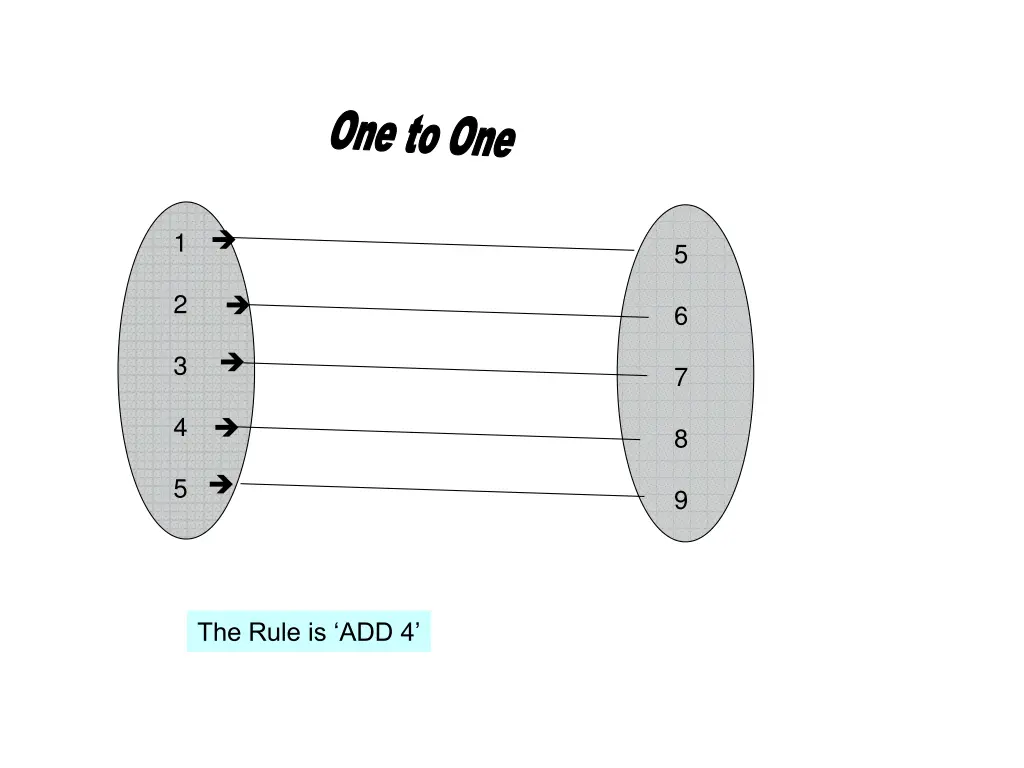
One to One 1 5 6 2 3 7 4 8 5 9 The Rule is ADD 4
Paris Ahmed London Peter Dubai Ali New York Jaweria Cyprus Hamad Has Visited There are MANY arrows from each person and each place is related to MANY People. It is a MANY to MANY relation.
Person Has A Mass of Kg Bilal 62 Peter Salma 64 Alaa George 66 Aziz In this case each person has only one mass, yet several people have the same Mass. This is a MANY to ONE relationship
Is the length of cm object Pen 14 Pencil Ruler Needle 30 Stick Here one amount is the length of many objects. This is a ONE to MANY relationship
FUNCTIONS Many to One Relationship One to One Relationship
x2x+1 A B 0 1 2 3 4 5 6 7 8 9 1 Image Set (Range) 2 3 4 Domain Co-domain
Functions - Notation f : x x2+ 4 f(x) = x2+ 4 The upper function is read as follows:- Function f such that x is mapped onto x2+4
Lets look at some function Type questions f(x) =x2+4 and g(x) =1 x2 If Find f(2) Find g(3) f(x) = x2+4 2 g(x) = 1 x2 = 8 = -8 2 3 3
Flow Diagrams Consider the function f(x) = 3x 1 We can consider this as two simpler functions illustrated as a flow diagram 3x x 3x 1 Multiply by 3 Subtract 1 Consider the function f : x (2x+5)2 (2x+5)2 2x+5 x 2x Square Multiply by 2 Add 5
Compound(Composite) Functions f : x 3x+2 and g(x) : x x2 Consider 2 functions fg is a composite function, where g is performed first and then f is performed on the result of g. The function fg may be found using a flow diagram 3x2+2 x 3x2 x2 Add 2 square Multiply by 3 f g Thus f g = 3x2+2
Composite Functions -Arrow Diagram 3x+2 x2 f g 2 14 4 2 fg(x) 3x2+2
Inverse Functions f(x) =5x 2 Consider the function 3 Here is its flow diagram f(x) =5x 2 5 -2 x 3 5 x Divide by three x Subtract 2 Multiply by 5 Draw a new flow diagram in reverse!. Start from the right and go left 3x+2 5 3x 3x+2 x Divide by 5 Multiply by three Add two f 1(x) =3x+2 And so 5
Which Are Functions? (b) (a) (d) (c) (a) and (c)
Which Are Functions? (b) (a) (d) (c) (a) and (c)
This powerpoint was kindly donated to www.worldofteaching.com http://www.worldofteaching.com is home to over a thousand powerpoints submitted by teachers. This is a completely free site and requires no registration. Please visit and I hope it will help in your teaching.