Understanding Geometric Series in Advanced Mathematics
Dive into the world of geometric series with Dr. Mazin R. Khalil in this advanced mathematics lecture. Learn about finite and infinite geometric series, common ratios, and methods of testing series. Explore examples and illustrations to enhance your understanding.
Uploaded on | 2 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Geometric Series Name of teacher :Dr. Mazin R Khalil Advanced Mathematics2 ME212 Semester 4 Week 3 Date: 13/2/2024
Objectives To teach students the following opinions through out the lecture: 1. Geometric series 2. Methods of testing series
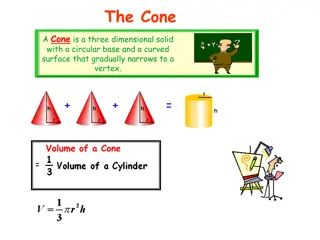
Geometric series A geometric series is the sum of finite or infinite terms of a geometric sequence. For the geometric sequence a, ar, ar2, ..., arn-1, ..., the corresponding geometric series is a + ar + ar2+ ..., arn-1+ .... We know that "series" means "sum". In particular, the geometric series means the sum of the terms that have a common ratio between every adjacent two of them. There can be two types of geometric series: finite and infinite. Here are some examples of geometric series. 1/2 + 1/4 + .... + 1/8192 is a finite geometric series where the first tern, a = 1/2 and the common ratio, r = 1/2 -4 + 2 - 1 + 1/2 - 1/4 + ... is an infinite geometric series where the first term, a = -4 and the common ratio r = -1/2
References 1. Thomas' Calculus" 11th edition 2. Calculus Early Transcendental Functions" by Ron Larson and Bruce Edwards