Understanding Hyperreals and Nonstandard Analysis
Explore the concept of hyperreals and nonstandard analysis, where a nonstandard universe exists with unique properties leading to the construction of a hyperreal field by using sequences of reals. Learn about the Transfer Principle and its implications, as well as the convenient use cases and significance of nonstandard extensions in simplifying complex proofs and linking analysis with model theory.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Nonstandard Analysis Student: Thomas Rainow Mentor: Krishan Canzius
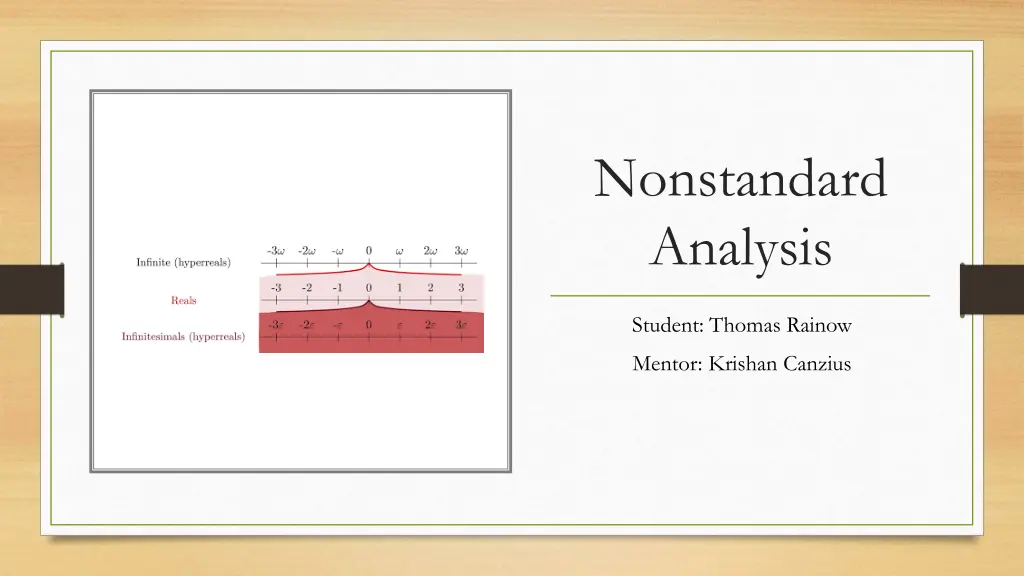
What are the hyperreals ? Suppose a nonstandard universe exists with four properties: is an ordered subfield of has a positive infinitesimal element ( ? ,? > 0,? < ? for every r? >0) For every function ?: ? , there is a natural extension ? ( )? , with the natural extensions of field operations behaves logically like
Turns out this exists! Let us construct a hyperreal field using sequences of reals We can use filters can think of these as a collection of big sets is an ultrafilter if for any A of , either A or \A is in the filter We can build equivalence classes on whether sequences agree on most elements through ultrafilters The set of equivalence classes under an ultrafilter is our nonstandard universe ( ?,+, ,0,1,<) is an ordered field and satisfies nonstandard properties
Transfer Principle Transfer principle: first-order statements transfer between the standard and nonstandard universes First order sentence: a sentence formed using logical symbols with no free variables Ex. ?? , ?? ? > ? Non example: ?? ? > ? Los Theorem proved the transfer principle for hyperreals Suppose we have an L-formula. Then the L-formula of sequences in the hyperreals is satisfied iff most individual elements satisfy the formula in the reals
More Transfer Principle Ex. ?? ,? ? ?? ,? ? The completeness axiom does not transfer { ??? ,? ??????? sup ? } { ??? ,? ??????? sup ? } { ??? ,? ??????? sup ? } { ???( ),? ??????? sup ? } Can think of transferring as adding asterisks everywhere in the sentence One common notation: ? ? ?,? are in the same cloud
Convenient Use Cases Standard Nonstandard Compactness Compactness Differentiability Differentiability
Why This Matters Oftentimes, making the nonstandard extension for functions is natural For every function ?: , we have an extension ? that behaves in the same way (ex. if ? is bounded, then ? is bounded) Can simplify convoluted proofs by transfer to nonstandard Formalizes logic around infinitesimals can simplify analysis Closely ties analysis and model theory
Thank You! Any questions?






















