Understanding Logarithms, Inverses, and L'Hopital's Rule
Explore the concepts of logarithms with base a, their inverses, common logarithms, and how to apply L'Hopital's Rule to evaluate limits. Discover examples and explanations for solving logarithmic equations and dealing with indeterminate forms in calculus.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
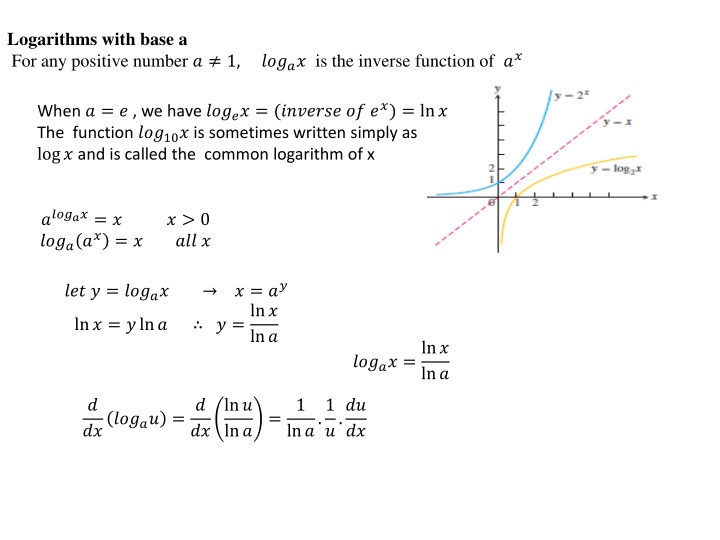
Logarithms with base a For any positive number ? 1, ????? is the inverse function of ?? When ? = ? , we have ????? = (??????? ?? ??) = ln? The function ???10? is sometimes written simply as log? and is called the common logarithm of x ??????= ? ??????= ? ? > 0 ??? ? ? = ?? ? =ln? ??? ? = ????? ln? = ?ln? ln? ????? =ln? ln? ? ?? ? ?? ln? ln? ln?.1 1 ?.?? ????? = = ??
Example: ? ?????10(3? + 1) ? ?? ln(3? + 1) ln10 1 1 3 = = ln10. (3? + 1).3 = ln 10 .(3? + 1) ???2? ? ?? Example: ln? ln2 ? ln2 ln? 1 = ?? = ?? ? ?? =?? ? = ln? ?2 2+ ? ? 1 1 = ln2 ??? = ln2 ???2 2 ???2 2ln2+ ? 1 = ln2. + ? = ?? ??= ?? Example:????? ? ? ???????????? ???????? ?? ?= ??? ? = ???+?= ???.?? ln? = ?? + ? ? = ? ???
???????: ????? ?3?4+ 5 = 2716 ?3? 4= 2711 ???3? 4= ln(2711) 3? 4 = ln(2711) 3? = ln 2711 + 4 ? =ln 2711 + 4 3 ???????: ????? 10?= 41 log10?= log41 ? = log41 = 3.968 ???????: ????? ?4?+ ?2? 6 = 0 ?2?+ 3 ?2? 2 = 0 ?2?+ 3 = 0 ?? ?2? 2 = 0 ?2?= 3 ?? ???????? ? =ln2 2 ?2?= 2 2? = ln2 = 0.347
?? ??= 1 + ? ?? , ? > 1 Example: ????? ? ? ???????????? ???????? ?? 1 + ?= ???? ln 1 + ? = ??+ ? ?? ??= ?(?2+ 1) Example: Solve the equation ? ? + 1 ? ? + 1 ?? = ? ?2+ 1 ?? ??? ?2+ 1= ??? ? + 1 ? 1 ? + 1= 1 ? + 1 ??? ?2+ 1= 1 1 ?? ? + 1 1 2ln 1 + ?2= ? ?? ? + 1 + ? ???????:????? log? + log3 = 2log4 log2 log3? = log16 log2 ???3? = ???16 2 ? =8 3? = 8 3
Indeterminate forms and Hopitals Rule Using Hopital s Rule to find the limits of some sequences Theorem ?? lim ? ? ? (?) ? (?) ?(?) ?(?)=0 ? ?? lim ?(?) ?(?)= lim 0 ?? ? ? ? ? sin2? ? ???????: ???? lim ? 0 0 0 ,??? ??????? ? ???? 2cos? 1 ?2+ ? 1 2?2+ 5 2? + 1 4? = = lim ? 0 = 2 ???????: ???? lim ? ??? ??????? ? ???? = ,??? ??????? ? ???? ?????? ???? = lim ? 2 4=1 = lim ? 2
? tan? sin? ? ???????: ???? lim ? 0 = 0 ,??? ??????? ? ???? 0 0 1 ???2? cos? 1 ??? ??????? ? ???? ?????? ???? 2sec?.sec????? sin? 1 ???2? ? 0 = lim ? 0 0 ? 0 ???2?tan? 1 ???3?= 2 = lim ? 0 = 2 lim sin? 1 = 2 lim cos?= 2 lim ? 0 ? Indeterminate form ? ? ?? ???????: ???? lim ? 0?ln? ln? 1 ? ,??? ??????? ? ???? = 0. ?? lim ? 0 1 ? lim ? 0 = lim ? 0 ? = 0 1 ?2
???????:???? lim 1 tan? sec2? ? ? 1 tan? 1 sec2? 4 1 tan? cos2? =0 0 ,??? ??????? ? ???? = 0. ?? lim = lim ? ? ? ? 4 4 1 ???2? 2sin2?= lim ???2? 2sin2?=2 = lim ? ? 2= 1 ? ? 4 4 ? Indeterminate form ? ?? 1 ? 1 ???????:???? lim ???? ? 0 ??? ? ? ???? ?=? ? ??? ??????? ? ???? = ?? = lim ? ? cos? 1 ???? ? + ????= 0 0 ,??? ??????? ? ???? ?????? ???? sin? ???? ? + cos? + cos?=0 = lim ? 0 = lim ? 0 2= 0
?2+ ? ? ???????:???? lim ? ?2+ ? + ? ?2+ ? ? . = ?? lim ?2+ ? + ? ? ?2+ ? ?2 ? = ??? ??????? ? ???? lim ? = lim ? , ?2+ ? + ? ?2+ ? + ? 1 = lim ? 1 1 2?2+ ? 1 2 2? + 1 + 1 1 =1 = lim ? = lim ? 2 +1 2? + 1 2? 1 +1 2 + 1 ? + 1 2 1 +1 ? ? ??? ???? ??, ? ,? 1 ? ???????: ???? lim ? 01 + ? 1 ? = 1 ? = 1 + ? ln? =1 ?ln 1 + ?
1 ?ln 1 + ? ??? ??????? ? ???? lim ? 0ln? = lim ln(1 + ?) ? ? 0 =0 = lim ? 0 0 , 1 1 + ? 1 = lim ? 0 lim ? 0ln? = 1 lim = 1 ? 0????= ? lim ? 0? = ? 1 ?= ? lim ? 01 + ? 1 ? ? 0??+ ? ???????: ???? lim = 1 ln? =1 ln(??+ ?) 1 ? ? = ??+ ? ?(??+ ?) =0 0 lim ? 0ln? = lim ? ? 0 1 ??+ ???+ 1 1 2 1 1= 2 lim ? 0ln? = lim = ? 0
lim ? 0ln? = 2 ? 0?ln ?= ?2 lim ? = ?2 1 ?= ?2 ? 0??+ ? lim