Understanding Quadratics: Investigating the Discriminant
Learn how to use the discriminant in quadratic equations to determine the nature of roots. Explore the impact of the discriminant on the graphs of various functions and its significance in solving equations. Use tools like Geogebra to deepen your understanding and draw conclusions about its effects.
Uploaded on | 2 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Quadratics The discriminant
Quadratics: The discriminant BAT know how to use the discriminant to solve problems and understand properties of quadratics KUS objectives Starter next page
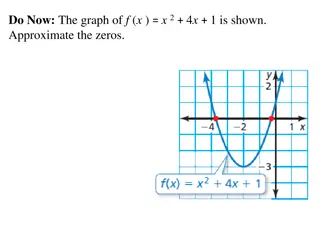
Challenge Investigate the Discriminant f(x) = x2 + 5x + 4 f(x) = x2 7x + 12 f(x) = x2 3x 28 f(x) = x2 6x + 9 f(x) = -x2 2x 1 f(x) = x2 + 3x + 5 f(x) = -x2 + 5x 11 f(x) = -x2 5x + 4 f(x) = 3x2 4x 3 f(x) = 4x 2x2 + 7 Investigate the discriminant . ?2 4?? Find out how it affects the graphs of the following functions. What conclusions can you come to about its effect? You may wish to use Geogebra or other graph drawing packages to help you. Work in your groups and allow at least a half hour to research and 1/2 hour to write up your conclusions
WB13 Use DESMOS or GEOGEBRA Draw these graphs use the formula to find the roots y = x2 - 4x +3 y = 3x2 -9x + 9 y =x2 + 4x + 4 What part of the formula tells you about the roots?
WB13 graphs y = x2 - 4x +3 y = 3x2 9x + 9 y =x2 + 4x + 4
WB13 conclusions x = -b b2 - 4ac 2a The bit in red is called the Discriminant if b2 - 4ac > 0 two distinct real roots crosses x axis twice if b2 - 4ac < 0 doesn t cross x axis No roots if b2 - 4ac = 0 Equal roots touches x axis once
WB 14 By evaluating the discriminant decide if the following have real and distinct roots b2 - 4ac = 1 real, distinct 1. 4x2 + 9x + 5 2. 5x2 4x + 2 3. 2x2 + 6x - 3.5 4. - 3x2 + 2x 1 5. 6x2 3x - 1 b2 - 4ac = -24 no roots b2 - 4ac = 64 real, distinct b2 - 4ac = -8 no roots b2 - 4ac = 33 real, distinct
WB 15a Given that the function ? ? = ?2+ ?? + 9 has equal roots find the possible values of p ?2 4?? = ?2 4 1 9 = 0 ?2= 36 ? = 6
WB 15b solve problem using the discriminant ?? ??? f(x) = 2x2 + 12x + c Given that f(x) = 0 has equal roots, find the value of c and hence solve f(x) = 0 ? =144 ?2 4?? = 144 4 2 ? = 0 = 18 8 ? ? = 2?2+ 12? + 18 ? ? = 2(?2+ 6? + 9) ? ? = 2 ? + 32 ? ? = 0 when ? = 3 DO NOT DO any more questions on the discriminant until you have covered quadratic Inequalities
KUS objectives BAT know how to use the discriminant to solve problems and understand properties of quadratics self-assess One thing learned is One thing to improve is