Understanding Triangle Similarity and Scale Factor Calculation
Explore various examples of similar triangles, learning how to find missing lengths using scale factor, common ratio, and Pythagoras Theorem. Discover the scale factor of enlargement and corresponding sides between similar shapes. Practice finding missing lengths and understanding the relationships between sides in similar triangles.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
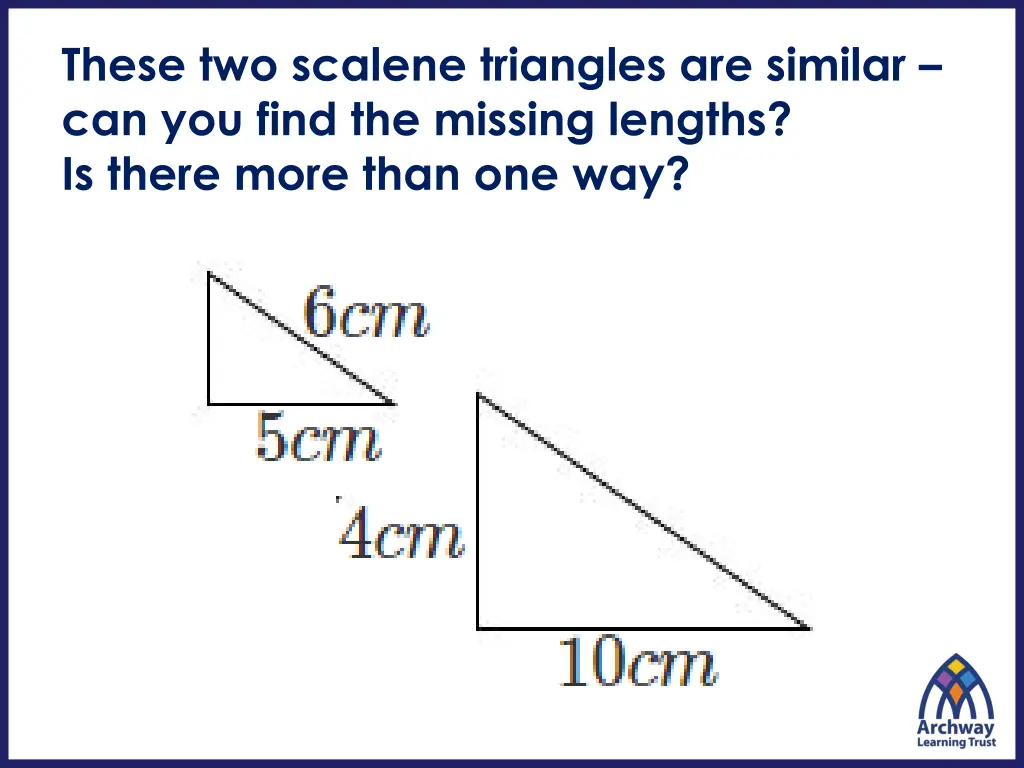
These two scalene triangles are similar can you find the missing lengths? Is there more than one way?
Using a scale factor Using a common ratio ? ? ? ? ?? =?2 =10 5= 2 ? 5 = 4 10 ?1 ? = 2?? ? = 6 2 = 12?? ? 10 = 6 5 ? = 4 2 = 2?? ? = 12cm
Sometimes the similar shapes will be within other shapes: Example Your turn 6m 8mm x2 4mm 6m 3m x2 8mm 5mm 5 x 2 = 10cm 7.5 x 2 = 15m 7.5m x x
What is the scale factor of enlargement between the two similar shapes? ?????????????=9 3=3 1= 3 3cm 9cm
What is the scale factor of enlargement between the two similar shapes? ?????????????=9 8= 11 8= 1.125 9cm 8cm
Multiple choice this time! What is the scale factor of enlargement between the two similar shapes? C C 8cm A D B B A 3cm E A E D 8 3 11 8 11 3 3 11 11 8 3 11 8 ?? ? 3
What is the scale factor between the two similar shapes? Hint: which are the corresponding sides? A B 6cm 3cm C 2 3cm D E
What are the missing lengths? Hint: which are the corresponding sides?
Find the size of ALL of the missing sides on these similar shapes. Is there more than one way? 15 3 4
Using a scale factor Using a common ratio 15 15 3 3 4 4 ?? ?? = ?? ?? ?? 15 = 4 3 ?? = 20?? ?? =?2 =15 3= 5 ?1 ?? = ?? 5 = 4 5 = 20?? ?? = ?? ?? = 20 4 = 16?? ?? = ?? ?? = 20 4 = 16?? Using Pythagoras Theorem, ?? = 5?? Using Pythagoras Theorem, ?? = 5?? ?? ?? = ?? ?? ?? 15 = 5 3 ?? = 25?? ?? = ?? 5 = 5 5 = 25?? ?? = ?? ?? = 25 5 = 20?? ?? = ?? ?? = 25 5 = 20??
Intelligent Practice Find the length of every missing side Triangles not drawn to scale 2. 1. 12mm x 20mm 4. 3. 6mm 6mm x x 6mm 12mm 10mm
Intelligent Practice Find the length of every missing side Triangles not drawn to scale 5. 6. 8mm 6mm 6mm x 3mm 12mm 6mm
Practice Find the length of every missing side Triangles not drawn to scale 2. 1. SF = 3 SF = 4 4x4=16mm 12mm x 20mm 5x3=15mm 4. 3. SF = 3 6mm 6mm SF = 2 x 6 2=3mm x 6 3=2mm 6mm 12mm 10mm
Practice Find the length of every missing side Triangles not drawn to scale 5. 6. SF = 1.5 8mm SF = 1.5 6mm 6mm x 8x1.5=12mm 12-8 = 4mm 6 1.5=4mm 3mm 6 1.5=4mm 12mm 6mm
1 2
Your Turn Complete the exam-style questions in the booklet provided.
?? = 12?? ?? = 5cm
?? = 18?? ?? = 10cm
Yes Angle EAC = Angle DBC (corresponding angles are equal) Angle AEC = Angle BDC (corresponding angles are equal) ?? = 39cm
165 133 82 72
No PQ = 25cm QR = 20cm 25 20 15 10
?? = 1.6cm Area D??? = 6.4 cm2
?? = 7.5?? ?? = 2.5cm ?? = 6cm ?? = 4cm Perimeter= 47cm ?? = 2cm