Understanding Vectors in Mathematics

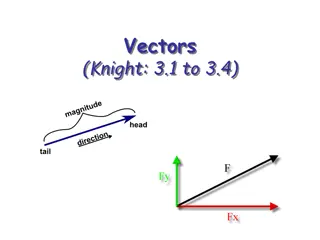
Vectors Twitter: @Owen134866 www.mathsfreeresourcelibrary.com

Prior Knowledge Check 3) In each triangle, find ? to one decimal place 1) Write the column vector for the translation of shape: a) A to B b) A to C c) A to D ? ? ? ? ???.? B 3 13 x ? ? 7 A 70 30 C x 9 ??.? D 8 7 2) P divides the line AB in the ratio AP:PB = 7:2. Find: a) ?? b) ?? 110 40 5 ?? c) ?? ?? ? ? x 18 ?? ? ? x ??.? ?.? ? ?

Teachings for Exercise 11A

Vectors A vector has both magnitude and direction. You can represent a vector using a directed line segment. A vector can be represented as a directed line segment Two vectors are equal if they have the same magnitude and direction 3a a Two vectors are parallel if they have the same direction C A You can add vectors using the triangle law of addition B ?? = ?? + ?? 11A

Vectors A Q C A vector has both magnitude and direction. You can represent a vector using a directed line segment. D a N OACB is a parallelogram. The points P, Q, M and N are the midpoints of the sides. M P OA = a O B b OB = b What can you deduce about AB and QN, looking at the vectors? Express the following in terms of a and b. a) OC a + b b) AB b - a c) QC 1/2b ?? =1 2? 1 ?? = ? ? 2? QN is a multiple of AB, so they are parallel! d) CN -1/2a e) QN 1/2b - 1/2a ?? =1 2(? ?) 11A

Vectors ?? =1 3?? A vector has both magnitude and direction. You can represent a vector using a directed line segment. A 1 ?? = 2? a N M In triangle OAB, M is the midpoint of OA and N divides AB in the ratio 1:2. OM = a OB = b 2 a O B b Use the ratio. If N divides AB in the ratio 1:2, show this on the diagram You can see now that AN is one-third of AB We therefore need to know AB To get from A to B, use AO + OB Express ON in terms of a and b ?? = ?? + ?? Sub in values ?? = 2? + 2 3? +1 ?? = ?? + ?? 3? Sub in AO and OB Simplify ?? = 2? + ? ?? =4 3? +1 3? AN = 1/3AB ?? = 2 3? +1 3? 11A

Teachings for Exercise 11B

Vectors (0,1) You can describe vectors using the i, j notation j A unit vector is a vector of length 1. Unit vectors along Cartesian (x, y) axes are usually denoted by i and j respectively. O i (1,0) C 5i + 2j ?? = ?? + ?? 2j You can write any two-dimensional vector in the form ai + bj ?? = 5? + 2? A B 5i -3i + j j Draw a diagram to represent the vector -3i + j -3i 11B

Vectors You can solve problems with vectors written using the i, j notation 2? ? = 2(5? + 2?) (3? 4?) Multiply out the bracket Careful with the subtraction here! Group terms 2? ? = 10? + 4? (3? 4?) When vectors are written in terms of the unit vectors i and j you can add them together by adding the terms in i and j separately. Subtraction works in a similar way. 2? ? = 10? + 4? 3? + 4? 2? ? = 7? + 8? You can also do these calculations using column vector notation! Given that: a = 5i + 2j b = 3i - 4j 2(5? + 2?) (3? 4?) As column notation Find 2a b in terms of i and j 3 25 4 2 11B

Teachings for Exercise 11C

Vectors 3i You can use Pythagoras Theorem to calculate the magnitude of a vector, and Trigonometry to calculate it s direction -7j 3i - 7j When a vector is given in terms of the unit vectors i and j, you can find its magnitude using Pythagoras Theorem. 32+ ( 7)2 ? = The magnitude of vector a is written as |a| Put in the values from the vectors and calculate ? = 58 Round if necessary Find the magnitude of the vector: 3i 7j ? = 7.62 (3sf) 11C

Vectors y You can use Pythagoras Theorem to calculate the magnitude of a vector, and Trigonometry to calculate it s direction Opp 5j 51.3 x -4i Adj Find the angle between the vector -4i + 5j and the positive x-axis Draw a diagram ???? =??? ??? Sub in values ???? =5 4 Inverse Tan The angle we want is between the vector and the positive x-axis Subtract from 180 ? = 51.3 ?????? ????? = 128.7 11C

Vectors y 10???30 5 You can use Pythagoras Theorem to calculate the magnitude of a vector, and Trigonometry to calculate it s direction 30 10???30 5 3 10 Vector a has magnitude 10 and makes an angle of 30 with j. Find a in column vector format. x You can again use GCSE trigonometry for this 5 = 5 3 11C

Teachings for Exercise 11D

Vectors You need to be able to use vectors to describe the position of a point in two dimensions A position vector tells you the position of a point from the origin The vector 2? + 3? could start anywhere The position vector 2? + 3? starts at (0,0) 11D

Vectors You need to be able to use vectors to describe the position of a point in two dimensions The position vector of a point A is the vector ??, where ? is the origin y y A A a B B b x x O O ?? = ?? + ?? ?? = ? + ? ?? = ?? ?? ?? = ? ? 11D

?? = ?? ?? Vectors y You need to be able to use vectors to describe the position of a point in two dimensions ? ? The points A and B in the diagram have coordinates (1,5) and (7,4) respectively. Find, in terms of ? and ?: a) The position vector of ? b) The position vector of ? c) The vector ?? O ?? = ? + 5? x ?? = ?? + 4? ?? = ?? ?? Sub in values ?? = (7? + 4?) (? + 5?) Simplify ?? = 6? ? 11D

?? = ?? ?? Vectors You need to be able to use vectors to describe the position of a point in two dimensions ?? = ?? ?? Sub in values 3? + 4? = ?? (5? 2?) Be very careful with the negatives here! 3? + 4? = ?? 5? + 2? ?? = 5? 2? and ?? = 3? + 4?. Find: Rearrange 8? + ?? = ?? a) The position vector of ? b) The exact value of ?? in simplified surd form (8)2+(2)2 ?? = Calculate ?? = 68 Simplify ?? = 2 17 11D

Teachings for Exercise 11E

?? = ?? ?? Vectors b - a A 1 You need to be able to use vectors to solve geometric problems and to find the position vector of a point that divides a line segment in a given ratio P 2 B a b O In the diagram the points A and B have position vectors a and b respectively. The point P divides line AB in the ratio 1:2. Find the position vector of P A good start is to write the vector we want in terms of others, and then work each of those out ?? = ?? + ?? Using the ratio, ?? must be 1 3?? ?? = ?? +1 3?? Fill in all the information on the diagram (including vector AB) Replace ?? ?? = ? +1 3? ? Multiply out Also indicate the ratio ?? = ? +1 3? 1 3? Simplify ?? =2 3? +1 3? 11E

?? = ?? ?? Vectors You need to be able to use vectors to solve geometric problems and to find the position vector of a point that divides a line segment in a given ratio A 3? 2? ? B ? 5? In triangle ???, ?? = 3? 2? and ?? = ? 5?. Find the size of ??? in degrees. 2? 3? C Start with a rough sketch We can use ?? and ?? to find ?? There are a number of ways you could approach this, using combinations of Pythagoras theorem and trigonometrical rules ?? = ?? ?? Sub in values ?? = (? 5?) (3? 2?) Calculate ?? = 2? 3? 11E

?? = ?? ?? Vectors You need to be able to use vectors to solve geometric problems and to find the position vector of a point that divides a line segment in a given ratio A c 3? 2? 13 ? B ? 5? 26 b In triangle ???, ?? = 3? 2? and ?? = ? 5?. Find the size of ??? in degrees. 2? 3? 13 a C We can find the magnitude of each side by using Pythagoras Theorem on each vector ?2= ?2+ ?2 2?????? Sub in values ( 13)2= ( 26)2+( 13)2 (2 26 13)???? Calculate parts 13 = 39 (26 2)???? Now we can use the cosine rule to find the angle Rearrange 2 = ???? 2 Inverse Cos ? = 45 11E

?? = ?? ?? Vectors You need to be able to use vectors to solve geometric problems and to find the position vector of a point that divides a line segment in a given ratio A a 13 ? B 90 26 c In triangle ???, ?? = 3? 2? and ?? = ? 5?. Find the size of ??? in degrees. 13 b C Was there a faster way we could have done it? Lets test Pythagoras Theorem ?2+ ?2= ?2 Sub in values 2+ 2= 2 13 13 26 Calculate parts 13 + 13 = 26 Since Pythagoras Theorem works, the triangle must be right-angled, with the longest side being the hypotenuse 11E

?? = ?? ?? Vectors You need to be able to use vectors to solve geometric problems and to find the position vector of a point that divides a line segment in a given ratio A 13 ? 45 B 90 26 In triangle ???, ?? = 3? 2? and ?? = ? 5?. Find the size of ??? in degrees. 13 45 ? C Was there a faster way we could have done it? Also, there are 2 sides the same length, so the triangle is also isosceles! This means that the other 2 angles will be equal! Be on the lookout for patterns in questions that can help you save time! 11E

?? = ?? ?? Vectors ?? = (? + ?) c A B You need to be able to use vectors to solve geometric problems and to find the position vector of a point that divides a line segment in a given ratio a P OABC is a parallelogram. P is the point where OB and AC intersect. O C The vectors a and c represent OA and OC respectively. c Prove that the diagonals bisect each other. One way to get from O to P Start with OB If the diagonals bisect each other, then P must be the midpoint of both AC and OB OP is parallel to OB so is a multiple of (a + c) ?? = ? + ? We don t know how much for now, so can use (lamda) to represent the unknown quantity Try to find a way to represent OP in different ways ?? = (? + ?) (make sure you don t accidentally assume P is the midpoint this is what we need to prove!) 11E

?? = ?? ?? Vectors ?? = (? + ?) ?? = ? + ?(? ?) A c B You need to be able to use vectors to solve geometric problems and to find the position vector of a point that divides a line segment in a given ratio a P -a OABC is a parallelogram. P is the point where OB and AC intersect. O The vectors a and c represent OA and OC respectively. C c Another way to get from O to P Go from O to A, then A to P We will need AC first Prove that the diagonals bisect each other. If the diagonals bisect each other, then P must be the midpoint of both AC and OB AP is parallel to AC so is a multiple of it. Use a different symbol (usually , mew , for this multiple) Now we have another way to get from O to P ?? = ? ? ?? = ?(? ?) Try to find a way to represent OP in different ways ?? = ?? + ?? (make sure you don t accidentally assume P is the midpoint this is what we need to prove!) Sub in vectors ?? = ? + ?(? ?) 11E

?? = ?? ?? Vectors ?? = (? + ?) ?? = ? + ?(? ?) A B You need to be able to use vectors to solve geometric problems and to find the position vector of a point that divides a line segment in a given ratio a P OABC is a parallelogram. P is the point where OB and AC intersect. O The vectors a and c represent OA and OC respectively. C ?? = (? + ?) As these represent the same vector, the expressions must be equal! ?? = ? + ?(? ?) Prove that the diagonals bisect each other. ? + ? = ? + ?(? ?) Multiply out brackets If the diagonals bisect each other, then P must be the midpoint of both AC and OB ? + ? = ? + ?? ?? Factorise the a terms on the right side ? + ? = (1 ?)? + ?? Now compare sides there must be the same number of a s and c s on each = 1 ? = ? Sub 2nd equation into the first Try to find a way to represent OP in different ways (make sure you don t accidentally assume P is the midpoint this is what we need to prove!) = 1 Rearrange and solve So P is halfway along OB and AC and hence the lines bisect each other! = 0.5 They are equal 11E = 0.5

Teachings for Exercise 11F

Vectors N 2km You need to be able to use vectors to solve problems in context. O A A girl walks 2km due east from a fixed point O to A, and then 3km due south from A to B. Find: 3km a) The position vector of B relative to O c) ?? d) The bearing of B from O The total distance travelled 5?? b) B Remember that this asks for the distance travelled, not the displacement! 2 + 3 = 5?? 11F

Vectors N 2km You need to be able to use vectors to solve problems in context. O A A girl walks 2km due east from a fixed point O to A, and then 3km due south from A to B. Find: 3km a) The position vector of B relative to O c) ?? d) The bearing of B from O The total distance travelled 5?? b) ?? = 2? 3? ?? B Consider the movement as i and j components ?? = 2? 3? ?? Make sure you include the units as this question has a context! 11F

Vectors N 2km You need to be able to use vectors to solve problems in context. O A A girl walks 2km due east from a fixed point O to A, and then 3km due south from A to B. Find: 3km a) The position vector of B relative to O c) ?? d) The bearing of B from O The total distance travelled 5?? b) ?? = 2? 3? ?? B ?? = 3.61 ?? You can use Pythagoras Theorem to find the magnitude (2)2+( 3)2 ?? = ?? = 3.61 ?? 11F

Vectors N 2km You need to be able to use vectors to solve problems in context. O A 56.3 A girl walks 2km due east from a fixed point O to A, and then 3km due south from A to B. Find: 3km a) The position vector of B relative to O c) ?? d) The bearing of B from O The total distance travelled 5?? b) ?? = 2? 3? ?? B ?? = 3.61 ?? You can find the value of ? using Trigonometry Also remember that bearings are always measured clockwise from north! ???? =3 2 Inverse Tan ? = 56.3 Add on the 90 from North ??????? = 146.3 Bearings are written as 3 digits ??????? = 146 11F

Vectors N You need to be able to use vectors to solve problems in context. 120 N O 15km 240 In an orienteering exercise, a cadet leaves the starting point O and walks 15km on a bearing of 120 to reach A, the first checkpoint. From A he walks 9km on a bearing of 240 to the second checkpoint, at B. From B, he returns directly to O. Find: A 9km B 13.0? 7.?? ?? Imagine just drawing the journey from O to A a) The position vector of A relative to O b) ?? c) The bearing of B from O The position vector of B relative to O We can then form a right angled triangle to work out the i and jcomponents d) N 120 N 15Cos30 13.0km O 30 7.5km 15Sin30 15km A 11F

Vectors N You need to be able to use vectors to solve problems in context. 120 N O 30 c 15km 60 240 In an orienteering exercise, a cadet leaves the starting point O and walks 15km on a bearing of 120 to reach A, the first checkpoint. From A he walks 9km on a bearing of 240 to the second checkpoint, at B. From B, he returns directly to O. Find: A 13.1km 60 a 9km b B 13.0? 7.5? ?? We can use the same right-angled triangle from part a) to help with part b) a) The position vector of A relative to O b) ?? c) The bearing of B from O The position vector of B relative to O 13.1km ?2= ?2+ ?2 2?????? d) Sub in values ?2= (15)2+(9)2 2(15)(9)???60 Calculate right side ?2= 171 Square root ? = 13.1?? 11F

Vectors N You need to be able to use vectors to solve problems in context. 120 N O 15km 36.6 ? 240 In an orienteering exercise, a cadet leaves the starting point O and walks 15km on a bearing of 120 to reach A, the first checkpoint. From A he walks 9km on a bearing of 240 to the second checkpoint, at B. From B, he returns directly to O. Find: A 13.1km 60 a 9km o B We need to find angle ?and then add on 120 to find the bearing of B from O ???? ? ? Sub in values (use the exact value for the length of side a) 13.0? 7.5? ?? a) The position vector of A relative to O b) ?? c) The bearing of B from O The position vector of B relative to O =???? 13.1km 157 d) ???? 9 =???60 171 Multiply by 9 ???? =9???60 171 Calculate right side ???? = 0.596 Inverse Sine ? = 36.6 Add on 120 ??????? = 157 11F

Vectors N You need to be able to use vectors to solve problems in context. 120 N O 15km 36.6 240 In an orienteering exercise, a cadet leaves the starting point O and walks 15km on a bearing of 120 to reach A, the first checkpoint. From A he walks 9km on a bearing of 240 to the second checkpoint, at B. From B, he returns directly to O. Find: A 13.1km 60 9km B 13.0? 7.5? ?? a) The position vector of A relative to O b) ?? c) The bearing of B from O The position vector of B relative to O N As in part A, consider a right angled- triangle drawn using OB as the hypotenuse 13.1km 157 120 d) O 36.6 24.4 We can work out an angle inside the triangle using the information we already have 5.1? 12.1? ?? 13.1km 12.1km 13.1Cos24.4 We can then find the horizontal and vertical distances, which are therefore the i and j components! B 13.1Sin24.4 5.1km 11F