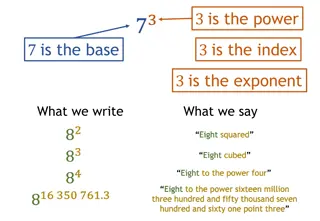
Unveiling Unique Mathematical Patterns Through Imagery
Explore a series of captivating mathematical patterns depicted through a collection of images. From intricate equations to visually stunning representations, dive into the intriguing world of mathematical artistry. Each slide unveils a new perspective, inviting you to contemplate the beauty of mathematics in a visual context.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
y ( ) f x = + '( )( f x ) y x x 0 0 0 ( ) f x ( ) f x = 0 x = x x 0 0
( ) ( ) ( ) x M ( ) ( ) ( ) p = f x p x 0 0 p x = f x 0 0 x = f 0 0 ( )( ) ( )( ) n n = f x p x 0 0
(x ) f n n a ( ) n ( ' ' ) ( ) f a f a + + + + 2 n ( ) ( ' )( ) ( ) ... ( ) f a f a x a x a x a ! 2 ! n
( 3 ) ( ' ' ) ( ) f a f a + + + + 2 3 ( ) ( ' )( ) ( ) ( ) ... f a f a x a x a x a ! 2 ! 3
( ) n ( ' ' ) ( ) f a f a + + + + 2 n ( ) ( ' )( ) ( ) ... ( ) f a f a x a x a x a ! 2 ! n ( 3 ) ( ' ' ) ( ) f a f a + + + + 2 3 ( ) ( ' )( ) ( ) ( ) ... f a f a x a x a x a ! 2 ! 3
+ 2 3 1 n n x x x x = + + + + + + + x 1 ... ... e x + ! 2 ! 3 ! ( 1 )! n n
2 . 1e 2 3 2 . 1 + 2 . 1 + = 2 . 1 + + 2 . 1 e 1 .......... ......... ! 2 ! 3 E 2 . 1e % a a
( ) 2! f a ( )( 2 ( ) f x = ( ) f a + - ) + ( - ) f a x a x a ) 3 ( ( ) f a + + 3 ( ) ... x a ! 3 n ) ( ( ) f a + + n ( ) x a R n ! n x n ( - ) x t = ( + 1) n ( ) t dt R f n ! n a
x a "( ) 2! f f x 2 ( ) = ( ) f x + '( )( x - ) + ( - ) i f x f x x x x + 1 + 1 + 1 i i i i i i i (3) ( ) n ( ) 3! ( ) ! n f x x 3 n + ( - ) + ... + ( - ) + i i x x x x R + 1 + 1 i i i i n
( 3 ) " ( ) ( ) f x ! f x = + + + 2 3 ( ) ( ) ( ' ) i i f x f x f x h h h + 1 i i i 2 ! 3 ( ) n ( ) f x + + + n ... i h R n ! n ) 1 + ( n ( ) f + = 1 n R h n + ( 1 )! n
(3) ( ) n ( ) 2! ( ) 3! ( ) ! n f x f x f x ( ) x h 2 3 n ( ) = ( ) f x + + + + ... + + i i i f x f h x h h R + 1 i i i n ( + 1) n ( ) 1)! f x + 1 n = R h n ( + n x
2 4 6 x x x = + + cos( ) 1 x ! 2 ! 4 ! 6 3 5 7 x x x = + + sin( ) x x ! 3 ! 5 ! 7 2 3 4 5 x x x x = + + + + + + ex 1 x ! 2 ! 3 ! 4 ! 5
( ) nP x ( ) x R n
( ) 2! ( ) 3! f x f x 2 3 ( ) ( ) f x ( ) x h + = + + + + L f x h f h h
2 3 4 5 h h h h ( ) ( ) f x ( ) x h ( ) x ( ) x ( ) x ( ) x + = + + + + + + L f x h f f f f f 2! 3! 4 5 2 3 4 5 h h h h ( ) ( ) 0 ( ) 0 ( ) 0 ( ) 0 ( ) 0 ( ) 0 0 + = + + + + + + L f h f f h f f f f 2! 3! 4 5
3 5 7 x x x sin x x = - + - + 3! 5! 7! + 2 1 n x n n n = ( 1) - forall x (2 + 1)! = 0
= ( ) T x x 1 3 x = ( ) T x x 3 3! 3 5 x x = + T x 5 3! 5!
= 1 . 0 . 0 5 . 0 . 0 2 . 1 + 4 3 2 ( ) 15 25 f x x x x x
= 1 . 0 . 0 5 . 0 . 0 2 . 1 + 4 3 2 ( ) 15 25 f x x x x x ( ) @ ( ) f x = 1.2 - 0.25 = 0.95 if = 1 f x h h + 1 i i
2 ( ) @ 1.2 - 0.25 - 0.5 = 0.45 if = 1 f x h h h + 1 i
Errors Reduced step size f(x) = 0.1x4 - 0.15x3 - 0.5x2 - 0.25x + 1.2
( ) 6 ( ) 4 = ( ) 4 f f = 74, 125 , f ( ) 4 ( ) 4 = x f f = ( ) x 30, = 4 6 f 2 3 h h ( ) ( ) f x ( ) x h ( ) x ( ) x + = + + + + L f x h f f f 2! 3! = , 4 x = = 6 4 2 h
2 3 2 2! 2 3! ( ) ( ) 4 ( ) 4 2 ( ) 4 ( ) 4 4 + 2 = + + + f f f f f 2 3 2 2! 2 3! ( ) 6 ( ) = 125 + 74 2 + 30 + 6 f = = + + + 125 341 148 60 8 ( ) 6 f = 4 x
1 = = expansion series Taylor Obtain of at 1 f(x) a x 1 x = = ( ) ) 1 ( 1 f x f x 1 2 = = ( ' ) ) 1 ( ' 1 f x f 2 x ) 2 ( ) 2 ( = = ( ) ) 1 ( 2 f x f 3 x 6 4 ) 3 ( ) 3 ( = = ( ) ) 1 ( 6 f x f 2 3 1 : ) 1 = ) 1 + ) 1 ) 1 + Taylor Series Expansion ( ( ( ( ... a x x x 37
= ( ) f x sin( ) x
p p n f (n)(x) f (n)( ) ( ) 4 an= f (n)( 1 1 a = )/n! 4 1 2 4 1 p sin = = 0 sin( ) x 2 0 0! 2 1 1 2 1 1 2 1 1 2 1 1 2 1 ( ) 1 p a = = cos( ) x cos = 1 4 1 2 1! 2 ( ) ( ) 1 p sin( ) x a = - sin = - 2 4 2 2 2! 1 p a = cos( ) x - cos = - 3 3 4 3! 2 ( ) 1 p a = sin( ) x sin = 4 4 4 2 4! 1 1 1 1 2 1 1 2 1 1 2 1 1 2 2 3 4 5 ( ) ( ) ( ) ( ) ( ) p p p p p + - - - - - + - + - - K x x x x x 4 4 4 4 4 2 3! 4! 5! 2 2
= ( ) cos( 2 ) f x x p = x 4
( ) f x ( ( ) ( )( ) x f x f x x x + - 0 - 0 0 ( 2 3 ) - ) x x x + ( ) + ( ) 0 0 f x f x 0 0 2! 3!
p p ( ) f x cos(2 ) cos 0 x f = = = 4 2 p p ( ) x 2sin(2 ) 2sin 2 f x f = - = - = - 4 2 p p ( ) x 4cos(2 ) 4cos 0 f x f = - = - = 4 2 p p ( ) x 8sin(2 ) 8sin 8 f x f = = = 4 2
( ) f x ( ) ( )( ) f x f x x x + - 0 - 0 0 ( 2 3 ( ) - ) x x x x + ( ) + ( ) 0 0 f x f x 0 0 2! 3! p ( ) f x 0 2 x - - 4 2 3 p p - - x x 4 4 0 8 + + 2! 3! 3 4 3 p p ( ) f x 2 x x - - + - 4 4
The exponentia function l computed is by 2 3 4 n x x x x = + + + + + + + x 1 ... ... e x 2 ! 3 ! 4 ! n x = 0.5
|a| < s s
= + ( ) sin( ) cos( 2 ) f x x x
2 x (0) ( ) f x (0) (0)2 f f x f + + ( ) ( ) ( ) sin( ) cos( ) sin( ) = - cos(2 ) 2sin(2 ) 4cos(2 ) - (0) (0) (0) 1 1 f x f f x x f = = + = = = - x x x x f f - 4 x x
2 ( ) f x 1 2 x x + - 2 (1.5) 1 1.5 + 2 (1.5) 2 f - = -
( )( x ( ) f x ( ) f x ) f x x + - 0 - 0 0 2 ( ) x x + ( ) 0 f x 0 2 p = = 1.5708... x 0 2