Using Decision Trees for Student Placement and Success Prediction
This presentation at the CAIR Conference delves into the application of decision trees in predicting student placement and course success, analyzing multiple measures, decision models, and tools in the educational context. It explores the integration of data analytics for supporting student success and highlights critiques of current placement systems.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Using Decision Trees to Predict Student Placement and Course Success CAIR Conference November 21, 2014
Todays Presentation Multiple Measures Project overview Overview of recursive partitioning Pros and cons of decision trees Use for placement Code for creating decision trees in R Comparison to logistic regression Fit statistics Pruning, bagging and random forests Decision trees and disproportionate impact
Multiple Measures Assessment Project Data warehouse Research base and predictive analytics K-12 messaging and data population Decision models and tools Professional development Pilot colleges and faculty engagement Integration with Common Assessment Key idea: less about testing more about placement and support for student success
Data Warehouse for MMAP Data in place K-12 transcript data CST, EAP and CAHSEE Accuplacer CCCApply MIS Other College Board assessments Local assessments Coming soon Compass Common Assessment and SBAC 5
Pilot Colleges Participating Allan Hancock Bakersfield College Ca ada College Contra Costa Community College District Cypress College Foothill-De Anza Community College District Fresno City College Irvine Valley College Peralta Community College District Rio Hondo College San Diego City College Santa Barbara City College Santa Monica College Sierra College
Placement at the CCCs Test-heavy process Placement cannot, by law, rely only on a test Multiple measures have traditionally involved a few survey-type questions More of a nudge than a true determinant Role of counselors Informed self-placement AP coursework & equivalencies
Validating Placement Tests Content validity Criterion validity Arguments-based validity Validating the outcome of the decision that is made based on the placement system/process Critiques of current placement system as prone to high degree of severe error (Belfield & Crosta, 2013; Scott-Clayton, 2012; Scott-Clayton, Crosta, & Belfield, 2012; Willett, 2013)
Decision Trees Howard Raiffa explains decision trees in Decision Analysis (1968). Ross Quinlan invented ID3 and introduced it to the world in his 1975 book, Machine Learning. Inspired by Hunt and others work in the 50 s & 60 s CART popularized by Breiman et al. in mid-90 s Breiman, L., Friedman, J., Olshen, R., & Stone, C. (1994). Classification and regression trees. Chapman and Hall: New York, New York. Based on information theory rather than statistics; developed for signal recognition Today we will discuss recursive partitioning and regression trees (i.e., rpart for R).
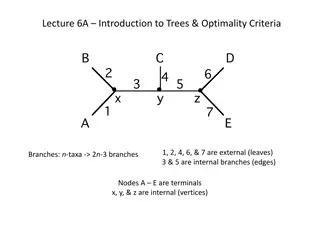
Increasing Homogeneity with each split A B Z Z A B Root Node B Z A Branch A B A ZZZ Internal Node B A B AAA BBB Leaf Node
How is homogeneity measured? ? ? 2 ? = ? = 1 ?? ?? ln ?? ?=1 ?=1 Gini-Simpson Index Shannon Information Index If selecting two individual items randomly from a collection, what is the probability they are in different categories. Measures diversity of a collection of items. Higher values indicate greater diversity. The Gini coefficient is a measure of the inequality of a distribution, a value of 0 expressing total equality and a value of 1 maximal inequality.
Pros and Cons of Decision Trees Strengths Visualization Easy to understand output Easy to code rules Model complex relationships easily Linearity, normality, not assumed Handles large data sets Can use categorical and numeric inputs Weaknesses Results dependent on training data set can be unstable esp. with small N Can easily overfit data Out of sample predictions can be problematic Greedy method selects only best predictor Must re-grow trees when adding new observations
Libraries and Code for R: Your Basic Classification Decision Tree Data <- read.csv( C:/Folder/Document.csv", header=T) Data.df <- data.frame(Data) DataTL <- (subset (Data.df,EnglishLevel== Transfer Level )) library(rpart) library(rpart.plot) ctrl <- rpart.control(minsplit = 100, minbucket = 1, cp = 0.001) DataTransferLevel <- (subset (Data.df,CourseLevel==1)) fitTL <- rpart(formula = success ~ Delay + CBEDS_rank + course_gp + A2G + cst_ss + grade_level + GPA_sans, data=DataTL, method = "class", control = ctrl) printcp(fitTL) prp(fitTL) rsq.rpart(fitTL) print(fitTL) print(fitTL, minlength=0, spaces=2, digits= getOption("digits")) summary(fitTL)
Decision tree predicting success in transfer-level English Misclassification=29% 1= Predicted success 0 = Predicted non-success GPA_sansis a student s cumulative high school GPA excluding grades in English. course_gis a student s grade in their most recent high school English course. Delay is the number of primary terms between last high school English course and first college English course. Note that GPA_sans was the most important predictor variable as determined by the random forest aggregated bootstrap method. 18
Decision tree predicting success in transfer-level Math Misclassification=36% 1= Predicted success 0 = Predicted non-success GPA_sansis a student s cumulative high school GPA without grades in math. hs_courseis a student s grade in most recent high school math course. Delay is the number of primary terms between last high school math course and first college math course. cst_ss is the scaled score from a student s California Standards Test (CST). CBEDS_ra is the rank or level of a student s last high school math course. Note that GPA_sans was the most important predictor variable as determined by the random forest aggregated bootstrap method. 19
Libraries and Code for R: Bagging and Random Forests library(ipred) btTL = bagging(cc_success ~ Delay + CBEDS_rank + course_gp + A2G + cst_ss + grade_level + GPA_sans, dat=DataTL,nbagg=30,method = "class",coob=T) print(btTL) library(randomForest) DataTL$cc_success <- factor(DataTL$cc_success) rfTL = randomForest(cc_success ~ Delay + CBEDS_rank + course_gp + A2G + cst_ss + grade_level + GPA_sans, dat=DataTL,importance=T,na.action=na.exclude,ntree=100) print(rfTL) importance(rfTL,type=1) varImpPlot(rfTL)
Key Considerations Splitting criterion: how small should the leaves be? What are the minimum # of splits? Stopping criterion: when should one stop growing the branch of the tree? Pruning: avoiding overfitting of the tree and improving Understanding classification performance
Two Approaches to Avoid Overfitting Forward pruning: Stop growing the tree earlier. Stop splitting the nodes if the number of samples is too small to make reliable decisions. Stop if the proportion of samples from a single class (node purity) is larger than a given threshold Post-pruning: Allow overfit and then post-prune the tree. Estimation of errors and tree size to decide which subtree should be pruned.
Fit Statistics: Evaluating your tree Misclassification rate - the number of incorrect predictions divided by the total number of classifications. Sensitivity - the percentage of cases that actually experienced the outcome (e.g., "success") that were correctly predicted by the model (i.e., true positives). Specificity - the percentage of cases that did not experience the outcome (e.g., "unsuccessful") that were correctly predicted by the model (i.e., true negatives). Positive predictive value - the percentage of correctly predicted successful cases relative to the total number of cases predicted as being successful. Negative predictive value - the percentage of correctly predicted unsuccessful cases relative to the total number of cases predicted as being unsuccessful.
Libraries and Code for R: Confusion Matrix pred=predict(fitTL,type="class") table(pred,e5$success) #pred=row,actual=col table(pred,e5$success,e5$gender) #by gender
Disproportionate Impact Renewed interest in equity across gender, ethnicity, age, disability, foster youth and veteran status Does a student s demographics predict placement level? If so, what is the degree of impact and what can be done to mitigate?
Combining Models How should multiple measures be combined with data from placement tests? Decision theory/Models for combining data Disjunctive (either/or) multiple measures as a possible alternative to the test Conjunctive (both/and) multiple measures as an additional limit Compensatory (blended) multiple measures as an additional factor in an algorithm
Does the Model Matter? Accuplacer Accuplacer Only Disjunctive A High Pass in English 12 or higher or Accupplacer Disjunctive B Pass in English 12 or higher or Accupplacer Conjunctive A High Pass in Fall and Spring English 12 or Higher Conjunctive B Pass in Fall and Accuplacer Placement From Willett, Gribbons & Hayward (2014)
Does the Model Matter? English 101 Placement 1000 899 Number of Students 749 800 600 475 343 400 228 200 0 Accuplacer Only Disjunctive A Disjunctive B Conjunctive AConjunctive B Model From Willett, Gribbons & Hayward (2014)
Thank you Craig Hayward Director of Planning, Research, and Accreditation Irvine Valley College chayward@ivc.edu John Hetts Senior Director of Data Science Educational Results Partnership jhetts@edresults.org Ken Sorey Director, CalPASS Plus ken@edresults.org Terrence Willett Director of Planning, Research, and Knowledge Systems Cabrillo College terrence@cabrillo.edu