Using Integration to Find Areas in Polar Coordinates

Teachings for Exercise 5C Teachings for Exercise 5C

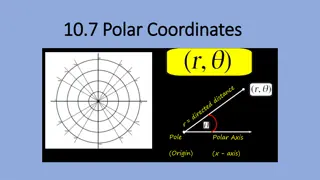
Polar Coordinates You can use Integration to find areas of sectors of curves, given their Polar equations Reminder of formula for the area of a sector, when ? is in radians A ? ? =1 2?2? O ? ? B 5C

? =1 2?2? Polar Coordinates You can use Integration to find areas of sectors of curves, given their Polar equations ?? Consider the area to the right, on the Polar equation ? = ?(?) ?? ? ?represents the area under the curve as in, between the curve and the half-lines ? = 0 and ? = ? ? = ?(?) ? If we increase ? by a small amount (??), it will also increase the area by a small amount (??) This new area will be between two values 5C

? =1 2?2? Polar Coordinates You can use Integration to find areas of sectors of curves, given their Polar equations ? = ?(?) ?? ? Consider the area to the right, on the Polar equation ? = ?(?) ? ?? ? ?represents the area under the curve as in, between the curve and the half-lines ? = 0 and ? = ? ? = ?(?) ? ?? 1 2?2 ?? In terms of ? If we increase ? by a small amount (??), it will also increase the area by a small amount (??) ?? 1 2?(?)2 ?? This new area will be between two values ?? 1 2?(?)2 ?? 5C

? =1 2?2? Polar Coordinates You can use Integration to find areas of sectors of curves, given their Polar equations ? = ?(? + ??) ?? ? Consider the area to the right, on the Polar equation ? = ?(?) ? ?? ? ?represents the area under the curve as in, between the curve and the half-lines ? = 0 and ? = ? ? = ?(?) ? ?? 1 2?2 ?? In terms of ? If we increase ? by a small amount (??), it will also increase the area by a small amount (??) ?? 1 2?(? + ??)2 ?? This new area will be between two values ?? 1 2?(?)2 ?? ?? 1 2?(? + ??)2 ?? 5C

? =1 2?2? Polar Coordinates 1 2?(?)2 ?? ?? 1 2?(? + ??)2 ?? Divide all parts by ?? You can use Integration to find areas of sectors of curves, given their Polar equations 1 2?(?)2 ?? ?? 1 2?(? + ??)2 Let ? 0 (remember this alters the notation) Consider the area to the right, on the Polar equation ? = ?(?) 1 2?(?)2 ?? ?? 1 2?(?)2 The logical conclusion is ?? ??=1 ?represents the area under the curve as in, between the curve and the half-lines ? = 0 and ? = ? 2?(?)2 Integrate both sides with respect to ? ? = 1 2?(?)2 ?? The half can be factored out ? =1 If we increase ? by a small amount (??), it will also increase the area by a small amount (??) 2 ?(?)2 ?? You will often see it with ? written instead ? =1 2 ?2 ?? This new area will be between two values ?? 1 2?(?)2 ?? So this is how we find the area under a Polar curve! ?? 1 2?(? + ??)2 ?? 5C

? ???? =1 ?2 ?? 2 Polar Coordinates ? 2 3 You can use Integration to find areas of sectors of curves, given their Polar equations 6 The process is similar to that of regular Integration for finding an area. 0, 2 To find the area enclosed by the curve, and the half lines = and = , you can use the formula below: ? = ? + ???? ? ???? =1 ?2 ?? 2 ? 3 2 (you might notice the 1/2r2 being familiar as the formula for the area of a sector) So for the example above, we would calculate the shaded area by doing: ? 31 + ????2 ?? =1 2 ? 6 5C

? ???? =1 ?2 ?? 2 Polar Coordinates ? 2 You can use Integration to find areas of sectors of curves, given their Polar equations We are going to find the area enclosed by the curve As the curve has reflective symmetry, we can find the area above the x-axis, then double it 0 Find the area enclosed by the cardioid with equation: 0, 2 r = a(1 + cos ) 3 2 Sketch the graph (you won t always be asked to do this, but you should do as it helps visualise the question ) So for this question: ? = ?(1 + ????) ? = 0 ? = ? We will now substitute these into the formula for the area, given earlier: ? ???? =1 ?2 ?? 2 ? 5C

? ???? =1 ?2 ?? 2 Polar Coordinates ? ? 1 2 You can use Integration to find areas of sectors of curves, given their Polar equations ?2 ?? As we will be doubling our answer at the end, we can just remove the 1/2 now to save us doing it later! ? ? ?2 ?? ? Sub in values Find the area enclosed by the cardioid with equation: ? 2 ?? ? 1 + ???? 0 Square it all r = a(1 + cos ) ? ?21 + ????2 ?? You can put the a2 term outside the integral, since it is a constant 0 Sketch the graph (you won t always be asked to do this, but you should do as it helps visualise the question ) ? = ?(1 + ????) ? ?2 1 + ????2 ?? Multiply the bracket out 0 ? ?2 1 + 2???? + ???2? ?? 0 ? = 0 ? = ? We will need to rewrite the cos2 term so we can integrate it (using standard patterns from the regular Maths course will not work here as we would get additional terms other than cos ) 5C

???2? = 2???2? 1 Polar Coordinates ? ???? =1 ?2 ?? 2 ? ? ?2 1 + 2???? + ???2? ?? You can use Integration to find areas of sectors of curves, given their Polar equations 0 Replace cos2 ? 1 + 2???? +1 2???2? +1 ?2 2 ?? 0 Group like terms Find the area enclosed by the cardioid with equation: ?3 2+ 2???? +1 ?2 2???2? ?? 0 Now we can think about actually Integrating! r = a(1 + cos ) To replace cos2 , we can use the formula for cos2 from Pure Maths Sketch the graph (you won t always be asked to do this, but you should do as it helps visualise the question ) ? = ?(1 + ????) ???2? = 2???2? 1 Add 1 ???2? + 1 = 2???2? Divide by 2 ? = 0 ? = ? 1 2???2? +1 2= ???2? 5C

???2? = 2???2? 1 Polar Coordinates ? ???? =1 ?2 ?? 2 ? ? ?2 1 + 2???? + ???2? ?? You can use Integration to find areas of sectors of curves, given their Polar equations 0 Replace cos2 ? 1 + 2???? +1 2???2? +1 ?2 2 ?? 0 Group like terms Find the area enclosed by the cardioid with equation: ?3 2+ 2???? +1 ?2 2???2? ?? Integrate each term with respect to , using the standard patterns technique 0 r = a(1 + cos ) ie) Think about what would differentiate to give these, then adjust it to give the correct coefficient ? 3 2? + 2???? +1 ?2 4???2? 0 Sketch the graph (you won t always be asked to do this, but you should do as it helps visualise the question ) ? = ?(1 + ????) Sub in and 0 in separately, and subtract 3 2? + 0 + 0 0 + 0 + 0 ?2 Calculate ? = 0 ? = ? 3??2 2 Show full workings, even if it takes a while. It is very easy to make mistakes here! 5C

? ???? =1 ?2 ?? 2 Polar Coordinates ? Think about plotting r = asin4 1 0 You can use Integration to find areas of sectors of curves, given their Polar equations Sin /2 3 /2 2 -1 Find the area of one loop of the curve with polar equation: From the Sine graph, you can see that r will be positive between 0 and As the graph repeats, r will also be positive between 2 and 3 , 4 and 5 , and 6 and 7 r = asin4 So we would plot r for the following ranges of 4 0 4 2 4 3 4 4 5 6 4 7 Start by sketching it 0 /4 /2 3 /4 5 /4 3 /2 7 /4 From the patterns you have seen, you might recognise that this will have 4 loops /2 /4 3 /4 Sometimes it helps to plot the limits for positive values of r on your diagram! 0 7 /4 5 /4 3 /2 5C

? ???? =1 ?2 ?? 2 Polar Coordinates ? /2 /4 3 /4 You can use Integration to find areas of sectors of curves, given their Polar equations 0 Find the area of one loop of the curve with polar equation: r = asin4 7 /4 5 /4 3 /2 Start by sketching it So the values we need to use for one loop are: ? =? ? = ????4? ? = 0 4 From the patterns you have seen, you might recognise that this will have 4 loops We will substitute these into the formula for the area ? ???? =1 ?2 ?? 2 We only need to sketch one loop as this is what we need to find the area of (so this saves time!) ? 5C

? ???? =1 ?2 ?? 2 Polar Coordinates ? ? 1 2 ?2 ?? You can use Integration to find areas of sectors of curves, given their Polar equations ? Replace r and the limits we worked out ? 4????4?2 ?? 1 2 0 Find the area of one loop of the curve with polar equation: Square the bracket ? 4?2???24? ?? 1 2 Similar to last time, you can take the a2 term and put it outside the integral 0 r = asin4 ? 4???24? ?? 1 2?2 ? =? ? = ????4? ? = 0 4 0 We will need to write sin24 so that we can integrate it (by writing is as sin or cos without any powers) 5C

???2? = 1 2???2? Polar Coordinates ? ???? =1 ?2 ?? 2 ? ? 4???24? ?? 1 2?2 You can use Integration to find areas of sectors of curves, given their Polar equations Replace sin24 0 ? 4 1 1 2?2 2(1 ???8?)?? Before integrating, you can take the 1/2 outside the integral as well 0 Find the area of one loop of the curve with polar equation: ? 41 ???8??? 1 4?2 0 r = asin4 Now this has been set up, we can actually Integrate it! ? =? ? = ????4? ? = 0 4 To replace sin24 , we can use another formula for cos2 from C3 ???2? = 1 2???2? Rearrange 2???2? = 1 ???2? Divide by 2 ???2? =1 21 ???2? Multiply the terms by 4 ???24? =1 2(1 ???8?) 5C

???2? = 1 2???2? Polar Coordinates ? ???? =1 ?2 ?? 2 ? ? 4???24? ?? 1 2?2 You can use Integration to find areas of sectors of curves, given their Polar equations Replace sin24 0 ? 4 1 1 2?2 2(1 ???8?)?? Before integrating, you can take the 1/2 outside the integral as well 0 Find the area of one loop of the curve with polar equation: ? 41 ???8??? 1 4?2 0 Integrate using the standard patterns technique Sub in /4 (subbing in 0 will cancel all terms, so we don t really need to work this part out r = asin4 ? 4 ? =? 1 4?2? 1 ? = ????4? ? = 0 8???8? 4 0 1 4?2? 4 1 Remember that if you have cos , you would need to sub in 0! Work out the exact value 8???2? =??2 16 Important points: You sometimes have to do a lot of rearranging/substitution before you can Integrate Your calculator might not give you exact values, so you need to find them yourself by manipulating the fractions 5C

? ???? =1 ?2 ?? 2 Polar Coordinates ? 2 You can use Integration to find areas of sectors of curves, given their Polar equations 2 ? = ? + ???? a) On the same diagram, sketch the curves with equations: 1 0, 2 3 r = 2 + cos r = 5cos 2 3 2 b) Find the polar coordinates of the intersection of these curves Start by plotting the graph of r = 2 + cos Use a table if it helps, to work out values when is 0, /2, and 3 /2 c) Find the exact value of the finite region bounded by the 2 curves 5C

? ???? =1 ?2 ?? 2 Polar Coordinates ? 2 You can use Integration to find areas of sectors of curves, given their Polar equations ( /4,5 2/2) 2 ? = ? + ???? 0 a) On the same diagram, sketch the curves with equations: 5 1 0, 2 3 r = 2 + cos r = 5cos ? = ????? 2 (7 /4,5 2/2) 3 2 b) Find the polar coordinates of the intersection of these curves Now plot the graph of r = 5cos A Cos graph may be useful here as some values will be undefined 1 0 c) Find the exact value of the finite region bounded by the 2 curves Cos /2 3 /2 2 -1 Work out values of cos for 0, /4 and /2, as well as 3 /2, 7 /4 and 2 (this way we will have enough points to use to work out the shape ) 5C

? ???? =1 ?2 ?? 2 Polar Coordinates ? 2 You can use Integration to find areas of sectors of curves, given their Polar equations (2.5, /3) ? = ? + ???? a) On the same diagram, sketch the curves with equations: 0, 2 r = 2 + cos r = 5cos ? = ????? (2.5,- /3) 3 2 b) Find the polar coordinates of the intersection of these curves To find the intersection, we can use the two equations we were given: 2 + ???? = 5???? Subtract cos c) Find the exact value of the finite region bounded by the 2 curves Using these values of , we can work out that r = 2.5 at these points 2 = 4???? Divide by 4 0.5 = ???? Inverse cos (and work out the other possible answer) ? =? 3, ? 3 5C

? ???? =1 ?2 ?? 2 Polar Coordinates ? 2 You can use Integration to find areas of sectors of curves, given their Polar equations (2.5, /3) ? = ? + ???? a) On the same diagram, sketch the curves with equations: 0, 2 r = 2 + cos r = 5cos ? = ????? (2.5,- /3) 3 2 b) Find the polar coordinates of the intersection of these curves The region we are finding the area of is highlighted in green We can calculate the area of just the top part, and then double it (since the area is symmetrical) c) Find the exact value of the finite region bounded by the 2 curves 5C

? ???? =1 ?2 ?? 2 Polar Coordinates ? 2 3 You can use Integration to find areas of sectors of curves, given their Polar equations ? = ? + ???? a) On the same diagram, sketch the curves with equations: 0 r = 2 + cos r = 5cos ? = ????? 3 2 b) Find the polar coordinates of the intersection of these curves You need to imagine the top part as two separate sections Draw on the limits , and a line through the intersection, and you can see that this is two different areas c) Find the exact value of the finite region bounded by the 2 curves 1) The area under the red curve with limits 0 and /3 2) The area under the blue curve with limits /3 and /2 We need to work both of these out and add them together! 5C

? ???? =1 ?2 ?? 2 Polar Coordinates ? 2 3 You can use Integration to find areas of sectors of curves, given their Polar equations ? = ? + ???? a) On the same diagram, sketch the curves with equations: 0 r = 2 + cos r = 5cos ? = ????? 3 2 b) Find the polar coordinates of the intersection of these curves For the red curve: ? = 2 + ???? For the blue curve: ? = 5???? c) Find the exact value of the finite region bounded by the 2 curves ? =? ? = 0 3 ? =? ? =? 3 2 5C

???2? = 2???2? 1 Polar Coordinates ? ???? =1 ?2 ?? 2 ? For the red curve: ? = 2 + ???? For the blue curve: ? = 5???? ? =? 3 You can use Integration to find areas of sectors of curves, given their Polar equations ? =? ? =? ? = 0 3 2 a) On the same diagram, sketch the curves with equations: ? 1 2 ?2 ?? Sub in the values from above Also, remove the 1/2 since we will be doubling our answer anyway! ? ? 32 + ????2 ?? r = 2 + cos r = 5cos 0 Square the bracket ? 34 + 4???? + ???2? ?? b) Find the polar coordinates of the intersection of these curves Replace the cos2 term with an equivalent expression (using the equation for cos2 above) 0 ? 3 4 + 4???? +1 2???2? +1 2 ?? c) Find the exact value of the finite region bounded by the 2 curves 0 Group like terms, and then we can integrate! ? 3 9 2+ 4???? +1 2???2? ?? Red curve first! Sub the values into the area equation 0 5C

???2? = 2???2? 1 Polar Coordinates ? ???? =1 ?2 ?? 2 ? For the red curve: ? = 2 + ???? For the blue curve: ? = 5???? ? =? 3 You can use Integration to find areas of sectors of curves, given their Polar equations ? =? ? =? ? = 0 3 2 a) On the same diagram, sketch the curves with equations: ? 3 9 2+ 4???? +1 2???2? ?? Integrate each term, using standard patterns where needed 0 r = 2 + cos r = 5cos ? 3 9 2? + 4???? +1 4???2? Sub in the limits separately (as subbing in 0 will give 0 overall here, we can just ignore it!) 0 9 2 ? 3 ? 3 +1 2? 3 b) Find the polar coordinates of the intersection of these curves + 4??? 4??? Calculate each part (your calculator may give you a decimal answer if you type the whole sum in) 3? 2+ 2 3 + 3 c) Find the exact value of the finite region bounded by the 2 curves 8 Write with a common denominator 12? 8 +16 3 3 + 8 8 Red curve first! Sub the values into the area equation Group up 12? + 17 3 8 5C

???2? = 2???2? 1 Polar Coordinates ? ???? =1 ?2 ?? 2 ? For the red curve: For the blue curve: ? = 5???? ? =? 3 You can use Integration to find areas of sectors of curves, given their Polar equations ???? =12? + 17 3 ? =? 8 2 a) On the same diagram, sketch the curves with equations: ? 1 2 ?2 ?? Sub in the values from above Also, remove the 1/2 since we will be doubling our answer anyway! ? ? 25????2 ?? r = 2 + cos r = 5cos ? 3 Square the bracket ? 225???2? ?? ? b) Find the polar coordinates of the intersection of these curves Replace the cos2 term with an equivalent expression (using the equation for cos 2 above) 3 ? 2 25 1 2???2? +1 ? ?? c) Find the exact value of the finite region bounded by the 2 curves 2 We can move the 1/2 and the 25 outside to make the integration a little easier 3 ? 2 ???2? + 1 ?? 25 2 ? Now we can do the same for the blue part 3 5C

???2? = 2???2? 1 Polar Coordinates ? ???? =1 ?2 ?? 2 ? For the red curve: For the blue curve: ? = 5???? ? =? 3 You can use Integration to find areas of sectors of curves, given their Polar equations ???? =12? + 17 3 ? =? 8 2 ? 2 ???2? + 1 ?? a) On the same diagram, sketch the curves with equations: 25 2 ? 3 Integrate each term, using standard patterns if needed ? 2 r = 2 + cos r = 5cos 25 2 1 2???2? + ?? Sub in the limits (we do need to include both this time as neither will cancel a whole section out!) 3 25 2 1 2???? +? 1 2???2? 3+? b) Find the polar coordinates of the intersection of these curves 2 3 Calculate each part as an exact value 25 2 ? 2 4+? 3 3 c) Find the exact value of the finite region bounded by the 2 curves Write with common denominators 25 2 6? 12 3 3 12+4? 12 Group up and multiply by 25/2 Now we can do the same for the blue part 50? 75 3 24 5C

???2? = 2???2? 1 Polar Coordinates ? ???? =1 ?2 ?? 2 ? For the red curve: For the blue curve: You can use Integration to find areas of sectors of curves, given their Polar equations ???? =12? + 17 3 ???? =50? 75 3 8 24 Add these two areas together to get the total area! a) On the same diagram, sketch the curves with equations: 12? + 17 3 8 +50? 75 3 24 r = 2 + cos r = 5cos Write with a common denominator 36? + 51 3 24 +50? 75 3 24 b) Find the polar coordinates of the intersection of these curves Add the numerators 86? 24 3 24 Divide all by 2 c) Find the exact value of the finite region bounded by the 2 curves 43? 12 3 12 These questions are often worth a lot of marks! Your calculate might not give you exact values for long sums, so you will need to be able to deal with the surds and fractions yourself! 5C