Vectors in Geometry: Parallelograms and Manipulations

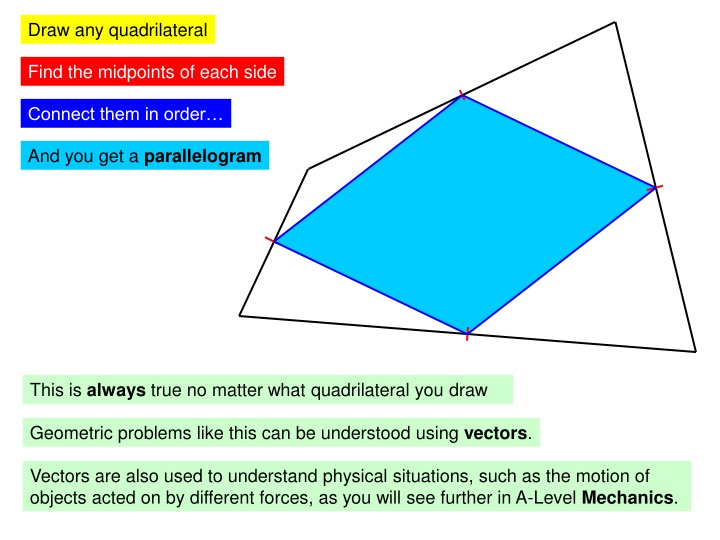
Draw any quadrilateral Find the midpoints of each side Connect them in order And you get a parallelogram This is always true no matter what quadrilateral you draw Geometric problems like this can be understood using vectors. Vectors are also used to understand physical situations, such as the motion of objects acted on by different forces, as you will see further in A-Level Mechanics.

What is a vector? A vector describes the direction and length of a movement You have already met column vectors when describing shape translations Vectors can also be represented by a single letter in bold or by the letters at the start and finish with an arrow above them 6 left, 1 down Eg PQRS is a parallelogram E a P D Q 0 left/right, 5 up b F Eg Write down the vector needed to translate from: 5 R S 0 6 = = = = a SR b PQ RQ SP F to E E to D 1

Column vectors Eg P is the point (1,5), Q is the point (9,3) R P a) Write down the vector PQ Write your answer as a column vector M Q 9 1 8 = = PQ 3 5 2 1 = QR PQR is a triangle. 3 M is the midpoint of PQ PR (b) Find the vector Write your answer as a column vector QM (b) Find the vector Write your answer as a column vector = + PR PQ QR 4 = 7 8 1 = QM PQ 1 = + = 2 1 2 3 1

Resultant vectors The outcome of a combination of vectors is called a resultant vector Eg If a and bare the vectors given below, draw diagrams to represent: i) a + 2b ii) b a iii) 3(a b) = 3a 3b b a a + 2b 3(a b) a + b means do a followed by b a - b means do a followed by b backwards a b Vectors can be manipulated algebraically

Resultant vectors Eg In the following diagram, write some equations about the vectors + = b = 3 + = a = 2 = + = d g e f b g a e c g a b d e c g b f d a

Vectors 1. The diagram shows two vectors a and b. a P b = a 2 + PQ b PQ On the grid above draw the vector

1 2 = = q p p q 2. p+ 3 q Write down as a column vector (i) (ii) 1 3 5 + 2 1 6 1 3 = = + = = 3 p q p q 10 + 3 1 9 1 2 R 3. The diagram is a sketch. P is the point (2, 3) Q is the point (6, 6) 0 = = PS QR 4 S Q a) Write down the vector PQ 0 4 Write your answer as a column vector 4 3 P 6 2 4 R is above Q = = PQ 6 3 3 Diagram NOT accurately drawn 4 = PR PQRS is a parallelogram. 7 4 4 0 = = + = + QS QP PS QS (b) Find the vector Write your answer as a column vector 1 3 4

Q Eg PQRS is a parallelogram. Find vectors for: R a X = a+ b = PQ + PR QR a) P S = a+ b = QP+ QS b b) PS ( ) =2 a+ = + b a b = 1 1 1 QS 1 c) QX where X is the midpoint of QS 2 2 2 = + = + = PQ + a a b a b 1 1 1 1 PX QX d) 2 2 2 2 Y is the point on the line RS such that 2RY = SY Q Find vectors for: R 1 a 3 X = a = 1 RY e) RS 1 Y 3 3 2 3 = b a = QR+ 1 P RY QY f) S b 3 ) ( + ) a ( = = + a b b a b 1 1 1 1 1 = XQ+ XY QY g) 2 2 3 6 2

4. PQRS is a trapezium. QP is parallel to RS. c R S = a = QR QP = 3RS c RS a 3 c Express in terms of a and/or c P Q (i)QP SP (ii) Diagrams NOT accurately drawn = 2 c = + a = = + + 3 c a c 3 c QP SP SR RO OP A = a OA 5. OAB is a triangle. P is the point on AB such that AP : PB = 2 : 1 OP = b OB a 2 3 Write in terms of a and b P = = + OP OA a AB a 2 3 1 ( ) O + + 3 b 2 b 3 + B = a b 1 2 3 3

= a = OP 6. OPQ is a triangle. T is the point on PQ for which PT : TQ = 2 : 1 b OQ Q 1 T 3 (a) Write down, in terms of a and b, an expression for PQ = PQ b 2 a+ 3 b O P a OT (b) Express in terms of a and b. Give your answer in its simplest form. Diagrams NOT accurately drawn ( ) = + = + a b = + 1 2 b a b 1 OT OQ QP 1 3 3 3 3 1 3 X B 7. OABC is a trapezium. OC is parallel to AB. a = OA 4 4 A = c OC AB = 2OC a X is the point on AB such that AX:XB = 3:1. XC Express in terms of a and c. O c C AX = = c 2 c 3 AB 2 = + = c c a c = + + 3 a 1 XC XA AO OC 2 2

Diagram NOT accurately drawn Eg OPQR is a trapezium with PQ parallel to OR. = = = 6 a 2 b 2 a OR OP PQ M a P Q M is the midpoint of PQ X Y 2 b N is the midpoint of OR 3 a R O N (a) Find the vector in terms of a and b. MN X is the midpoint of MN Y is the midpoint of QR. (b) Prove that XY is parallel to OR. = = = + + 3 MN MP a 2 2 PO 2 + b ON a b a = + + XY XM MQ QY = + + MN MQ QR 1 1 2 2 2 lines AB and CD are parallel if CD k AB = for some value k = = + + + 2 a b a a b 2 a = a 2 4 b = = + 6 a 2 2 6 a b a OR QR = 3 OR XY

Eg OAC, OBX and BQC are all straight lines C = = 4 a 4 = b OA 2 OB : 8 a = 1: 3 AC OA BQ QC and 3 2 4 3 (a) Find, in terms of a and b, the vectors which represent: A Q 4 a 1 1 3 4 = b 12 4 + = BO + a OC BC (i) X O 4 8 b b B = + AQ AB BC 1 (ii) = 8 b BX Given that (b) show that AQX is a straight line. 4 = + + 4 4 3 a b b a =3 b a = = = AO + a 12 4 + ( b 3 4 OX AX b 3 points ABC are on a straight line if AB k AC = for some value k ) a = 4 AX AQ and AQX is a straight line.

8. OABC is a parallelogram. P is the point on AC such that AP = 2 AC 3 A B = = 6 a OA 6 c OC OP 2 (a) Find the vector Give your answer in terms of a and c 3 6 a M P 1 = = + + OP OA 6 2 + = AC ( c 2 3 3 2 ) c 6 + 6 a a 4 a O 6 C c 3 The midpoint of CB is M. (b) Prove that OPM is a straight line. ( ) c ) c = a 2 + ( a 2 3 = 2 OP CM = 3 a = 6 a CB As parallelogram, = + OM = + OM OC CB 1 3 OM OP 2 a 2 = c 3 6 + and OPM is a straight line.

a C 9. CDEF is a quadrilateral with a = CD DE D = = a b b FC a b 1 M CE (a) Express in terms of a and b. a+ = CE 5 b 4 X b 5 (b) Prove that FE is parallel to CD. E F ( ) 2 a = = + + 2 a a b a b = + + FE FC CD DE = CD 2 FE so parallel Diagram NOT accurately drawn M is the midpoint of DE. (c) Express in terms of a and b. FM = 2 a b = + 1 FM FE EM 2 X is the point on FM such that FX : XM = 4 : 1 (d) Prove that C, X and E lie on the same straight line. ( ) ( ) ( ) = + + 42 = + =5 a+ a b a b a b b 3 3 3 = + 1 CX CF FM 4 5 2 5 5 5 = a+ = b CE 3 CX CE and CXE is a straight line. 5

10.The diagram shows a regular hexagon ABCDEF with centre O. 3 2 = = 6 6 a b OA OB A B 5 Y 5 (a) Express in terms of a and/or b X 6 b 6 a = a 6 6 + b (i) AB F C O = = (ii) EF 6 a OA X is the midpoint of BC. D E EX (b) Express in terms of a and/or b = + = 12 b 3 a EX EB BX Y is the point on AB extended, such that AB : BY = 3:2 (c) Prove that E, X and Y lie on the same straight line ( ) = + = + + 12 4 4 b a b EY EB AB 2 = 16 b 4 a 3 ( ) a ( ) a = b 4 3 EX = b 4 = 4 EY EY EX 4 and EXY is a straight line. 3 A regular hexagon can be split into 6 equilateral triangles

Proving that the midpoints of any quadrilateral form a parallelogram using vectors C = EB+ = b+ BF EF a 1 F = + HG HD DC G 2 a 1 = + + 2 2 2 ( ) c c b a B 2 c b D = = + c a b a b EF = HG = EA+ AH 1 EH = b+ c E H = + FG FC CD 2 c 1 = + + + 2 2 2 ( ) a a b c 2 a A = + + a b c Therefore 2 pairs of opposite sides with the same length and direction - a parallelogram! EH = = b+ FG c

Vectors 1. The diagram shows two vectors a and b. a P b = a 2 + PQ b PQ On the grid above draw the vector

1 2 = = q p p q 2. p+ 3 q Write down as a column vector (i) (ii) 1 3 3. The diagram is a sketch. P is the point (2, 3) Q is the point (6, 6) Q a) Write down the vector PQ Write your answer as a column vector P Diagram NOT accurately drawn 4 = PR PQRS is a parallelogram. 7 QS (b) Find the vector Write your answer as a column vector

4. PQRS is a trapezium. QP is parallel to RS. c R S = a = QR QP = 3RS c RS a Express in terms of a and/or c P Q (i)QP SP (ii) Diagrams NOT accurately drawn A = a OA 5. OAB is a triangle. P is the point on AB such that AP : PB = 2 : 1 OP = b OB a Write in terms of a and b P O b B

= a = OP 6. OPQ is a triangle. T is the point on PQ for which PT : TQ = 2 : 1 b OQ Q T (a) Write down, in terms of a and b, an expression for PQ b O P a OT (b) Express in terms of a and b. Give your answer in its simplest form. Diagrams NOT accurately drawn X B 7. OABC is a trapezium. OC is parallel to AB. a = OA A = c OC AB = 2OC a X is the point on AB such that AX:XB = 3:1. XC Express in terms of a and c. O c C

8. OABC is a parallelogram. P is the point on AC such that AP = 2 AC 3 A B = = 6 a OA 6 c OC OP (a) Find the vector Give your answer in terms of a and c 6 a P O 6 C c The midpoint of CB is M. (b) Prove that OPM is a straight line.

a C 9. CDEF is a quadrilateral with a = CD DE D = = a b b FC a b M CE (a) Express in terms of a and b. b X (b) Prove that FE is parallel to CD. E F Diagram NOT accurately drawn M is the midpoint of DE. (c) Express in terms of a and b. FM X is the point on FM such that FX : XM = 4 : 1 (d) Prove that C, X and E lie on the same straight line.

10.The diagram shows a regular hexagon ABCDEF with centre O. = = 6 6 a b OA OB A B (a) Express in terms of a and/or b X 6 b 6 a (i) AB F C O (ii) EF X is the midpoint of BC. D E EX (b) Express in terms of a and/or b Y is the point on AB extended, such that AB : BY = 3:2 (c) Prove that E, X and Y lie on the same straight line