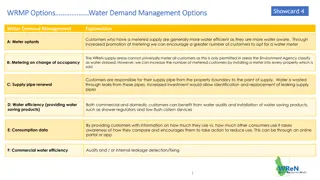
Understanding Efficiency of Algorithms and Approximations
Efficiency of algorithms can be approximated using Big-O, Big-Omega, and Big-Theta notations, facilitating the evaluation of computer program performance. Real functions can be categorized based on their order with respect to other functions, enabling the determination of performance characteristics. Examples demonstrate the application of these concepts in analyzing functions and justifying their classification.
Understanding Efficiency of Algorithms and Approximations
PowerPoint presentation about 'Understanding Efficiency of Algorithms and Approximations'. This presentation describes the topic on Efficiency of algorithms can be approximated using Big-O, Big-Omega, and Big-Theta notations, facilitating the evaluation of computer program performance. Real functions can be categorized based on their order with respect to other functions, enabling the determination of performance characteristics. Examples demonstrate the application of these concepts in analyzing functions and justifying their classification.. Download this presentation absolutely free.
Presentation Transcript
Chapter 9 Efficiency of Algorithms
9.2 Big-O, Big-Omega & Big-Theta
Approximations of Real Functions The O (big-O), (big Omega), and (big theta) are methods for approximating real functions. These approximations can be used to determine the efficiency of computer programs via approximation.
Approximations of Real Functions Approximations 1. For large values of x, the values of f(x) are less than those of a multiple of g(x), then f is of order at most g, or f(x) is O(g(x)). 2. For large values of x, the values of f(x) are greater than those of a multiple of g(x), then f is of order at least g, or f(x) is g(x)). 3. For large values of x, the values of f(x) are bounded both above and below by those of a multiple of g(x), then f is of order g, or f(x) is (g(x)).
Definition Let f and g be real-valued functions defined on the same set of nonnegative real numbers. Then 1. f is of order at least g, written f(x) is (g(x)), if, and only if, there exist a positive real number A and a nonnegative real number a such that A|g(x)| |f(x)| for real nums x>a 2. f is of order at most g, written f(x) is O(g(x)), if, and only if, there exist a positive real number B and a nonnegative real number b such that |f(x)| B|g(x)| for real nums x>b 3. f is of order g, written f(x) is (g(x)), if, and only if, there exist positive real numbers A and B, and a nonnegative real number k such that A|g(x)| |f(x)| B|g(x)| for real nums x > k
Example Express in theta notation 10|x6| 17x6 45x3+ 2x + 8 30|x6| for all real x>2. Recall: A|g(x)| |f(x)| B|g(x)| for real nums x>k A=10, B=30, g(x)=x6f(x)=17x6 45x3+ 2x + 8 17x6 45x3+ 2x + 8 is (x6) Express in omega notation 15|x1/2| Recall: A|g(x)| |f(x)| for real nums x>a A=15, a=0, g(x)=x1/2 is (x1/2)
Example Express in Big-OO notation 45 |x1/2|, x > 6 Recall: |f(x)| B|g(x)| for real nums x>b B=45, b=6, g(x)=x1/2 is O(x1/2)
Example Justify the statement is (x) given the previous two examples. 15|x1/2| 45|x1/2| Recall:A|g(x)| |f(x)| B|g(x)| for real nums x > k k must be the largest real number that satisfies the conditions, hence, x>0 and x>6 will require k=6. A=15, B=45 A|x1/2| B|x1/2|
Properties of O, , -Notations Theorem 9.2.1 Let f and g be real-valued functions defined on the same set of nonnegative real numbers. 1. f(x) is (g(x)) and f(x) is O(g(x)) if, and only if, f(x) is (g(x)). 2. f(x) is (g(x)) if, and only if, g(x) is O(f(x)). 3. f(x) is O(f(x)), f(x) is (g(x)), and f(x) is (f(x)) 4. If f(x) is O(g(x)) and g(x) is O(h(x)), then f(x) is O(h(x)). 5. If f(x) is O(g(x)) and c is any nonzero real number, then cf(x) is O(g(x)). 6. If f(x) is O(h(x)) and g(x) is O(k(x)), then f(x) + g(x) is O(G(x)) where G(x) = max(|h(x)|, |k(x)|) for each x in the domain of the functions. 7. If f(x) is O(h(x)) and g(x) is O(k(x)), then f(x)g(x) is O(h(x)k(x)).
Orders of Power Functions If 1 < x, then x < x2, x2< x3 . So, if 1 < x < x2< x3 For any rational numbers r and s if 1 < x, and r < s, then xr < xs(9.2.1) if r < s, then xris O(xs)
Example Show that for any real number x, if x > 1, then 3x3+ 2x + 7 12x3 From previous slide, x is real number and x > 1. Then x < x3and 1 < x3 So 2x < 2x3and 7 < 7x3(from LS 3x3+ 2x + 7) Add up inequalities: 3x3 3x3, 2x < 2x3and 7 < 7x3 3x3+ 2x + 7 3x3+ 2x3+ 7x3= 12x3
Example Show that 2x4 + 3x3+ 5 is (x4) by using the def s of big-Omega, big-O, and big theta. Solution f(x) = 2x4 + 3x3+ 5, g(x) = x4 for x > 0, 2x4 2x4 + 3x3+ 5 b/c 3x3+ 5 > 0 2|x4| |2x4 + 3x3+ 5|, A = 2, and a = 0 A|x4| |2x4 + 3x3+ 5|, for all x > a by definition of Omega-notation, 2x4 + 3x3+ 5 is (x4)
Example (cont) Previous can be expanded for O-notation Solution x > 1 and by 9.2.1 2x4 + 3x3+ 5 2x4 + 3x4+ 5x4 2x4 + 3x3+ 5 10x4 |2x4 + 3x3+ 5| 10|x4| Let B = 10 and b = 1, |2x4 + 3x3+ 5| B|x4| for all x > b. by definition of O-notation 2x4 + 3x3+ 5 is O(x4) Since 2x4 + 3x3+ 5 is both (x4) and (x4) then it is by definition O(x4).
Example Show that 3x3 1000x -200 is O(x3) by definition of O- notation. Solution |a + b| |a| + |b| for all real numbers (triangle inequality) further, |a - b| |a + (-b)| |a| + |-b| |a| + |b| for x>1, |3x3 1000x -200| |3x3| + |-1000x|+ |-200| |3x3 1000x -200| 3x3+ 1000x + 200 |3x3 1000x -200| 3x3+ 1000x3+ 200x3| |3x3 1000x -200| 1203x3 Let B = 1203 and b=1 then, |3x3 1000x -200| Bx3for all real numbers x > b So, by definition |3x3 1000x -200| is O(x3)
Example Show that 3x3 1000x 200 is O(xs) for s > 3 Recall that O(g(x)) bounds (top) f(x) Solution s > 3, then x3< xsfor all real numbers x>1 So, B|x3| < B|xs| for all real numbers x > 1 (b=1) |3x3 1000x -200| Bxsfor all real numbers x > b. Hence, by definition of O-notation, 3x3 1000x 200 is O(xs) for s > 3 .
Polynomial Orders Theorem (9.2.2) On Polynomial Orders Suppose a0, a1, a2, , anare real numbers and an 0. 1. anxn+ an-1xn-1+ + a1x + a0 is O(xs) for all ints s n. 2. anxn+ an-1xn-1+ + a1x + a0 is (xr) for all ints r n. 3. anxn+ an-1xn-1+ + a1x + a0 is (xn).
Example Find the orders for the functions f(x) = 7x5+ 5x3 x + 4, for all real numbers x solution: f(x) is (x5) g(x) = , for all real numbers x solution: (x-1)(x+1) = x2 1, g(x) is (x2)
Limitation of Orders of Polynomial Theorem: Limitation on Orders of Polynomial Functions (9.2.3) Let n be a positive integer, and let a0, a1, a2, , an be real numbers with an 0. if m is any integer with m < n, then anxn+ an-1xn-1+ + a1x + a0 is not O(xm), and anxn+ an-1xn-1+ + a1x + a0 is not (xm)
Example Show that 1 + 2 + 3 + + n is (n2) Solution 1 + 2 + 3 + + n = n(n + 1)/2 n(n + 1)/2 = n2/2 + n/2 Hence, n2/2 + n/2 is (n2) Therefore, 1 + 2 + 3 + + n is (n2)