Derivatives of Inverse Hyperbolic Functions
This content covers the derivatives of inverse hyperbolic functions such as sinh^(-1)x, cosh^(-1)x, tanh^(-1)x, sech^(-1)x, cosech^(-1)x, coth^(-1)x. Learn how to find and derive these functions with detailed explanations and examples.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
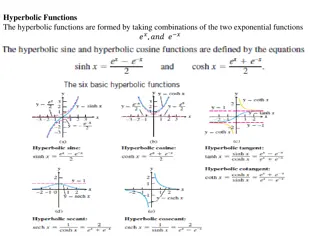
Derivatives of Inverse Hyperbolic functions We are familiar with hyperbolic functions. We learnt how to find the derivative of hyperbolic functions. Now we have to find the derivatives of Inverse hyperbolic functions i.e. Sinh-1x, cosh-1x, tanh-1x, sech-1x, cosech-1x, coth-1x these are inverse hyperbolic functions.
f Derivative of sinh 1? ???? =??? 1? ? =??? ? ?? =??? ? ?? ?? 1 = ?? ??? ? Since ??? 2? ??? 2? = 1
???2? = 1+???2? ??? ? = 1+??? 2? ?? ??= 1 1+??? 2? ?? ??= 1 1+?2 Where the sign of radical is same that of cosh? which we know cosh???always +?? ? ??(sinh 1?) = 1 1+?2
Derivative of tanh1?.[ ? < 1] Let y= tanh 1? ? = tanh ? ?? ?? = sech2? ?? 1 ?? = sec h2? Since sech2? + tanh2? = 1 sech2? = 1 tanh2? ?? 1 ?? = 1 tan h2? ?? 1 ??= ? ??(tanh 1?)= 1 ?2 1 1 ?2
Type equation here.Derivative of sech 1? Let y = sech 1? X = sech? ?? ?? = -sech?tanh? ?? ?? = 1 sech ? tanh ? We know that sech2? + tanh2? = 1 ??? 2y = 1-??? 2y tanh? = 1 ??? 2? ?? 1 ?? = sech ? 1 ??? 2?
= Where the sign of radical is same that of tanh y but we know that sech 1? is always +ve. tanh 1????????? + ??.
j Derivative of cosech 1? Let y = cosech 1? ? = cosech? ?? ?? = - cosech?coth? ?? ??= 1 cosech?coth? We know that ??? 2y ????? 2? = 1 ??? 2? = 1 + ????? 2? coth? = 1 + ????? 2? ?? ??= 1 cosechy1 +????? 2? 1 ? ??cosech 1? = |x| ?2+1 Type equation here.
Where the sign of radical is same that of coth y, coth y is +ve or ve according to value of x. Similarly we can find the derivative of cosh 1? &coth 1?