Digital Signal Processing with Dr. Michael Nasief: Understanding Convolution and Fourier Analysis
In this educational content, Dr. Michael Nasief explores key concepts in digital signal processing, focusing on topics like convolution, Fourier analysis, frequency response, and complex values. Through detailed explanations and visual aids, learners can grasp the fundamentals of finite-length sequences, convolution properties, and the discrete-time Fourier transform. The content delves into the implications of convolving finite and infinite-length sequences, emphasizing the importance of understanding signal processing principles to analyze and manipulate signals effectively.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Digital Signal Processing Dr. Michael Nasief Lec 5 1
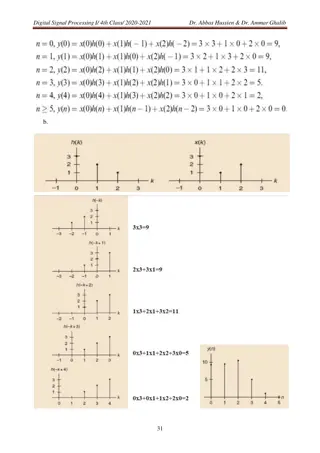
Ex 1 The first nonzero value of a finite-length sequence x(n) occurs at index n = -6 and has a value x(-6) = 3, and the last nonzero value occurs at index n = 24 and has a value x(24) = -4. What is the index of the first nonzero value in the convolution 2
Ex 2 The convolution of two finite-length sequences will be finite in length. is it true that the convolution of a finite-length sequence with an infinite-length sequence will be infinite in length? It is not necessarily true It may be either 3
EX 3 Convolve 4
Because h(n) is equal to zero outside the interval [-3, 3], and x(n) is zero outside the interval [l, 5], the convolution y(n) = x(n) * h(n) is zero outside the interval [-2, 8]. 6
Ex 4 10
Chapter [2] Fourier Analysis 12
FREQUENCY RESPONSE FREQUENCY RESPONSE Signals of the form 13
THE DISCRETE THE DISCRETE- -TIME FOURIER TRANSFORM TIME FOURIER TRANSFORM The discrete-time Fourier transform (DTFT) of a sequence, x(n), is defined as In order for the DTFT of a sequence to exist, the summation in Eq. (2.3) must converge. This, in turn, requires that x(n) be absolutely summable: 15
EXAMPLE EXAMPLE 16
IDTFT 17