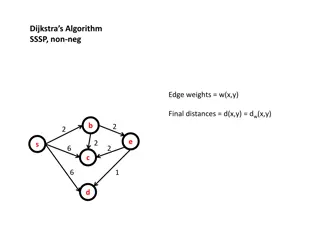
Dijkstra's Algorithm for Shortest Path Problems
"Learn about Dijkstra's algorithm, a greedy strategy for solving the Single-Source Shortest Path problem. Explore correctness proofs, running time analysis, and a specialized implementation called Dials. Visual examples and detailed explanations included."
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Dijkstras algorithm Solves SSSP when ? ?,? 0 ?,? ? A greedy strategy
Correctness (1) THM: When ? is added to ?, ?.? = ?(?,?) Proof. Induction on adding vertices to ? Base: ?.? = ? ?,? = 0 Step: If ? ?,? = then ?.? = (upper bound property) Assume ? ?,? < . Let ? be a shortest path from ? to ?
Correctness (2) Let ? be the first vertex on ? which is not in ? By the induction assumption: ?.? = ?(?,?) ?.? ?.? + ? ?,? = ? ?,? + ? ?,? = ?(?,?) ?.? ?.? = ? ?,? ? ?,? ?.? = ?(?,?)
Running time We perform ? delete operations from ? and ? decrease-key operations (implicit in relax) ? ? + ? log? with binary heaps and ? ?log? + ? with Fibonacci heaps
Dials implementation The algorithm is similar to BFS which take ?(?) time Can we speed it up if all weights are small integers say 0,1,2, ,? ? Lem (monotonicity): If ?1 is added to ? before ?2 then ? ?,?1 ? ?,?2 Allocate an array ? of size (? 1)?. Put ? ? in ?[?.?] Maintain a pointer ? to ?[?.?] where ? is the last node added to ? Extract-min: Increment ? until reaching a nonempty cell of ? return an element from this cell
y z 3 1 2 t 2 0 1 3 s 2 3 x u 2 s 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 (? 1)? p W=3
y z 3 1 1 2 t 2 0 1 3 s 2 3 3 x u 2 y x 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 (? 1)? p W=3
y z 3 1 1 2 t 2 0 1 3 s 2 3 3 x u 2 y x 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 (? 1)? p W=3
y z 3 1 4 1 2 t 2 0 1 3 s 2 3 2 x 3 u 2 x u z 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 (? 1)? p W=3
y z 3 1 4 1 2 t 2 0 1 3 s 2 3 2 x 3 u 2 x u z 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 (? 1)? p W=3
y z 3 1 4 1 2 t 2 0 1 3 s 2 3 2 x 3 u 2 u z 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 (? 1)? p W=3
y z 3 1 4 1 2 t 2 0 1 3 s 2 3 2 x 3 u 2 u z 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 (? 1)? p W=3
y z 3 1 4 1 2 t 2 0 5 1 3 s 2 3 2 x 3 u 2 z t 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 (? 1)? p W=3
Analysis of Dials implementation ? ? + ?? Space ? ?? Very fast if ? is small