Dynamic Linear Programming in Minimum Spanning Tree Problem
Explore dynamic linear programming formulations for the Minimum Spanning Tree problem, detailing the algorithm steps and arc connections. Witness examples and images illustrating the process and optimization.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
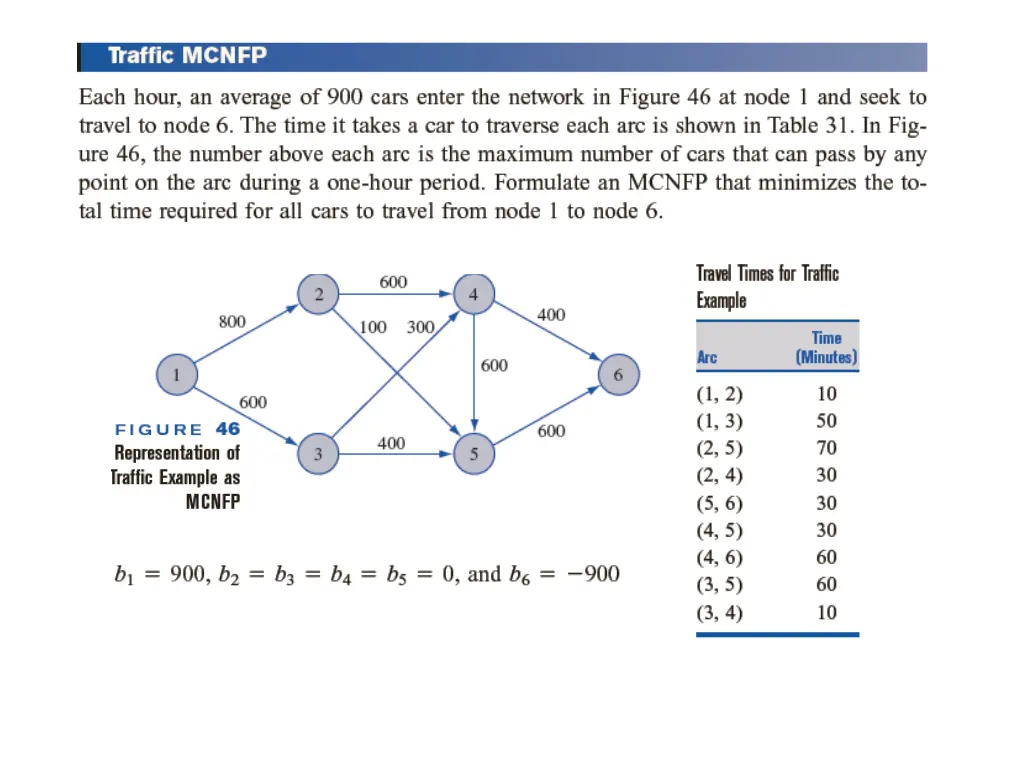
+ + + + + + + + + 10 50 30 70 10 60 30 60 30 Min S t x x x x x x x x x x 12 13 x 24 25 34 35 45 46 56 = . 900 0 0 0 0 = 600 600 0 12 x 13 + + = = x x 12 24 25 + + x x x x 13 34 35 + + = = x x x 24 34 45 x 46 + x x x x 25 35 45 56 900 800 600 600 100 300 400 600 x 46 56 x 12 x 13 x 24 x 25 x 34 x 35 x 45 x 46 x 56 , , , , , , , , x x x x x x x x x 12 13 24 25 34 35 45 46 56
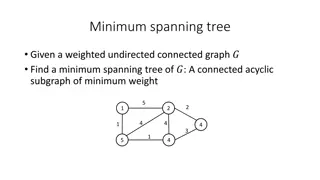
Linear Programming of a Minimum Spanning Tree Problem k E j At each general step of the above algorithm if denoted all of the arc which connected and means that then the following dynamic linear programming can consider as the formulation of Minimum Spanning Tree problem: C k = {( , ) i j | , } E A i C C C k k k k C Min d x l k ij ij ( , ) i j E i dij k . 1 , 1 S t x C N k ij K ( , ) i j E s k {0,1}, ( , ) x i j E j ij k m k C k
Example for formulation of Minimal Spanning Tree + + + + + + 4 6 3 2 + 4 Min S t x x x x x x x 13 x x 14 23 x x 35 x x 45 + . 1 13 14 x 23 35 45 x , , , , {0,1} 13 14 23 35 45