Efficient Algorithms for Optimal Perimeter Guarding - Problem Description and Examples

Efficient Algorithms for Optimal Perimeter Guarding Si Wei Feng , Shuai D. Han , Kai Gao and Jingjin Yu Department of Computer Science, Rutgers University at New Brunswick, Piscataway, New Jersey, U.S.A. School of Mathematical Sciences, University of Science and Technology of China, Hefei, Anhui, China Rss 2019: http://rss2019.informatik.uni-freiburg.de/papers/0007_FI.pdf Full paper at: https://arxiv.org/abs/1905.04434

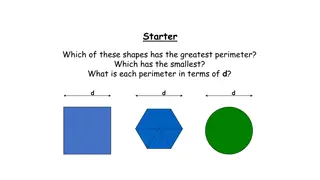
Problem description and examples The optimal Perimeter Guarding (OPG) problem is to find the best partition to regions s.t. the maximal region a robot needs to guard is minimized.

Basic notations ? - number of robots ? - number of regions ??- number of connected components in region ?

Notations ? regions ? = ?1, ,?? ???is ??boundary ??? ?1 ?? = ??1, ,??? ?? ???is called the perimeter of ?? ??is the part covered by robot ? in a given cover ? is the maximal length of any ??in an optimal cover

Optimal Perimeter Guarding (OPG) Given the perimeter .

Perimeters Containing Single Components

Perimeters Containing Single Components

Perimeters Containing Single Components In a potential optimal solution: For a given region ??, each of the ??robots assigned to guard it must each guard a length ??= ???(??)/?? For (at least) one region ??, it holds that ??= ? (the maximal single robot coverage length) Thus, one can try for each ??all possible 1 ?? ? and find the minimum ??= ???(??)/??that is feasible. Such ??and ??will be named ?? ? will be the smallest among all computed ?? ?and ?? ?respectively. ?.

Improvements ?the minimum Can use binary search over 1 ?? ? to find ?? ???(??)/??that is feasible for a given region ?? If we start by first examining the longest ??, only up to one candidate ?? produce a better result (? ). ?per any remaining region ??has the potential to

Examining the longest ??first Assume ?1is the longest perimeter Not feasible Doesn t improve result over ?1 ?

Perimeters Containing Single Components Running time: ?(? log ? + log ? )

Perimeters Containing Single Components

Single Perimeter Containing Multiple Components

Single Perimeter Containing Multiple Components We Know how to cover multiple regions without gaps, why not think of every connected component as a single region without gaps?

Lemma No gap needs to be partially covered by a robot For a perimeter ?, there exists an optimal cover ? = ?1 ?? , ,?? ? = ? ?? ?? such that, for any gap ? and any ? = ? , ??

Notations 2.0 Let a perimeter ? have ? segments ?1, ,?? which are divided by ? gaps {?1, ,??} Example: A region with five segments ?1, ,?5and five gaps ?1, ,?5

Proposition 2 - Some gap must be skipped

Proposition 3 - There are OPG instances in which the biggest gap must be covered. The optimal cover with ? = 3 is to have ? = {?1,?2,(?3 ?3 ?4)} In ? we have ? = ???(?1) Red cover: l = ??? ?1 Blue cover: ? 3??? ?1+0.5??? ?1 blue cover is worse 3 ??? ?3 = 1.5???(?1)

Theorem 5

Single Perimeter Containing Multiple Components A baseline algorithm: For all 1 ?,? ? denote the part of ?? from ??to ?? following a clockwise direction and including the gaps as Skk len Skk nkk the biggest ??? s.t. the len Skk nkk Theorem 5 states that for some 1 ?,? ?, = l c c To find ? , for each 1 ?,? ? we find nkk problem is feasible and compute lkk c = c c is ? The smallest lkk Running time O(?2 ?) O(feasibility check)

feasibility check For checking feasibility of a particular ??? i.e., whether ??? is long enough for the rest of the robots to cover the rest of the perimeter we simply tile ? ??? copies of ??? over the rest of the perimeter. Thus time complexity is O ?2 ? O(q) = O(?3 ?)

Variants and results multiple perimeters with each having a single connected component ?(? log ? + log ? ) ?(? log ? + log ? ) multiple perimeters with each having a single connected component single perimeter containing multiple connected components ?(?2log ? + ? ) ?(?2log ? + ? ) single perimeter containing multiple connected components multiple perimeters with each containing multiple connected components ? 1 ? ??? ? 1 ? ??? multiple perimeters with each containing multiple connected components 2log ? + 1 ? ??? 2log ? + 1 ? ???

Thank you for your time