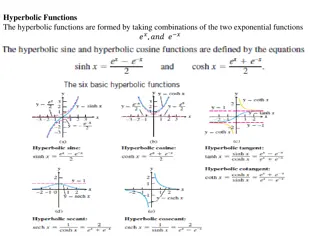
Inverse Function Derivatives Relationship Explained
Understand the relationship between the derivatives of a function and its inverse, showcasing that they are reciprocals of each other at corresponding points. Explore how the slopes of f and f^-1 are related through visuals and linear function properties.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
The derivatives of f and f -1 How are they related?
(4,6) Recall that if we have a one-to- one function f, we get f -1 from f, we switch every x and y coordinate. f -1 (2,3) (6,4) f (3,2) (-1,-1)
Inverses of Linear functions = + = ( ) f x mx b 1( ) x ??? f = + y mx b 1 m ( ) = y b x
Inverses of Linear functions 1 m ( ) = + = x b 1 ( ) f x mx b ( ) x f = + y mx b In other words, the inverse of a linear function is a linear function and the slope of the function and its inverse are reciprocals of one another. 1 m ( ) = y b x
f -1 Slope is 1 m f Slope is m.
What about the more general question? What is the relationship between the slope of f and the slope of f -1? f -1 (2,3) f (3,2)
Note: the points where we should be comparing slopes are corresponding points. E.g. (3,2) and (2,3). f -1 (2,3) f (3,2)
What happens when we zoom in on these points? f -1 (2,3) f (3,2) We see straight lines whose slopes are reciprocals of one another!
f -1 In general, what does this tell us about the relationship between and ? f f ( ) 1 (b, f -1(b)) ( ) f Slope is . f a (a, f (a)) 1 ( ) f a ( ) = 1 ( ) b f
f -1 In general, what does this tell us about the relationship between and ? f f ( ) 1 (b, f -1(b)) f (a, f (a)) = (f -1(b), b) 1 ( ) f a ( ) = 1 ( ) b f But a = f -1(b), so . . . 1 ( ) = 1 ( ) b f 1 ( ( )) b f f
Upshot If f and f-1 are inverse functions, then their derivatives at corresponding points are reciprocals of one another : 1 ( ) = 1 ( ) x f 1 '( ( )) x f f
Derivative of the logarithm 1 ( ) f a 1 ea 1 e ( ) = 1 ( ) b f f (x) = e x = (a, e a) 1 b = = ln( ) f -1(x) = ln(x) b (b, ln(b)) 1 x d dx = ln( ) x