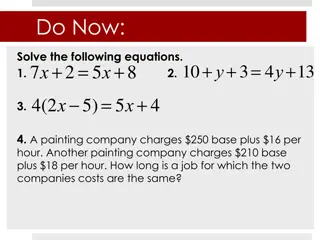Solving Multi-Step Equations in Integrated Mathematics

1 / 24

Embed Share

"Learn to solve multi-step equations in integrated mathematics by separating, simplifying, determining variable placement, and solving for the unknown. Practice with examples provided to enhance understanding."

kcost Follow

Uploaded on Apr 13, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

Download Presentation

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

E N D

Presentation Transcript

Solving Multi-Step Equations INTEGRATED MATHEMATICS

Objectives Students will calculate the value of an unknown term of a multistep equation through the combination of like-terms.

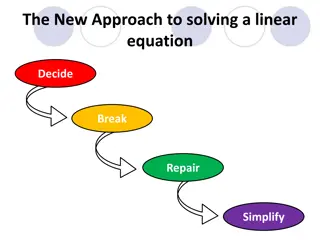
Multi-Step Equations 1) Separate the Equation 2) Simplify A) Distributive Property B) Combine Like-Terms 3) Should It Stay or Should It Go (Variables on Left/Constants on Right) 4) Solve for Variable

Multi-Step Equations Ex. 1) 7? + 3 4? + 1 = 10

Multi-Step Equations Ex. 2) 4? 1 + 3? = 10

Multi-Step Equations Ex. 3) 29 = 6? + 5 4 + ?

Multi-Step Equations Ex. 4) 2? + 4 x 3 = 18

Multi-Step Equations Ex. 5) 135 = 3 1 5? 8?

Multi-Step Equations Ex. 6) 9 = 7 7? 1 + 2(? + 1)

Multi-Step Equations Ex. 7) 5 6? 1 5 1 + 8? = 70

Try These 1. 4? 10 1 3? = 20 2. 42 = 5(8n 1)2(n 2) 3. 4? 10 1 3? = 20 4. 2(3p + 1) 4(2 3p) = 50

Multi-Step Equations 1) Separate the Equation 2) Simplify A) Distributive Property B) Combine Like-Terms 3) Should It Stay or Should It Go (Variables on Left/Constants on Right) 4) Solve for Variable

Multi-Step Equations Ex. 9) 3 + 5? = 6? 7 2?

Multi-Step Equations Ex. 10) 7? + 3 = 2(5? + 3)

Multi-Step Equations Ex. 11) 3(7 + 2x) = 30 + 7(x 1)

Multi-Step Equations Ex. 12) 4(3 + 5y) 4 = 3 + 2(y 2)

TRY THESE 1) 8? + 6 2? = 12 4? 2 2) 4d 8 d = 6 - d 3) 3 ? + 4 5 = 5 + 12 4) 4v + 5v 4 = 10 + 3v 5. ? ? ?? = ?(? + ?) 6. ? ? ? + ? ? + ? = ? ?

Objectives Students will calculate the value of an unknown term of a multistep equation through the combination of like-terms. Students will differentiate between equations that have no solution and an infinite number of solutions.

Solutions to Linear Equations Solutions to Linear Equations An equation with one variable may have: Exactly One Real Solution Infinite Real Solutions (Identity) No Real Solution